43. The density function of a chi-squared random variable having n degrees of freedom can be shown to be

where (t) is the gamma function defined by

Integration by parts can be employed to show that (t) = (t−1)(t−1), when t > 1.
If Z and χ2 n are independent random variables with Z having a standard normal distribution and χ2 n having a chi-square distribution with n degrees of freedom, then the random variable T defined by

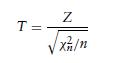
is said to have a t-distribution with n degrees of freedom. Compute its mean and variance when n > 2.

f(x) = x/2(x/2)* (n/2) x>0