94. Let N be a hypergeometric random variable having the distribution of the number of white balls in a random sample of size r from a set of w white and b blue balls.

That is,

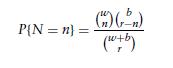
where we use the convention that mj
= 0 if either j m. Now, consider a compound random variable SN = Ni =1 Xi , where the Xi are positive integer valued random variables with αj = P{Xi = j}.

(a) With M as defined as in Section 3.7, find the distribution of M − 1.

(b) Suppressing its dependence on

b, let Pw,r(k) = P{SN = k}, and derive a recursion equation for Pw,r(k).

(c) Use the recursion of

(b) to find Pw,r(2).

P{N=n} = (m) (ron) (w+b)