(a) Take first and second derivatives with respect to time of q given in Eq. (30.28), and...

Question:

(a) Take first and second derivatives with respect to time of q given in Eq. (30.28), and show that it is a solution of Eq (30.27).

(b) At t = 0 the switch shown in Fig. 30.17 is thrown so that it connects points d and a; at this time, q = Q and i = dq/dt = 0. Show that the constants Ï• and A in Eq. (30.28) are given by

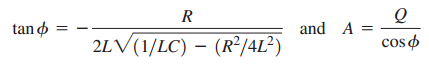
tan o and A = 2LV(1/LC) – (R²/4L²) cos o

Fig 30.17

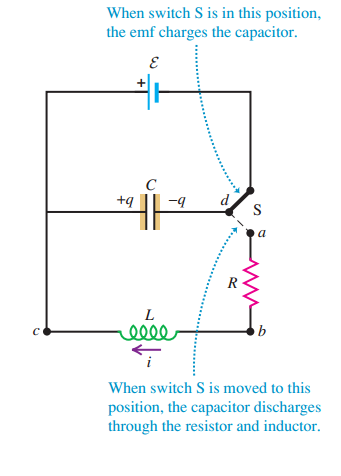
When switch S is in this position, the emf charges the capacitor. +q el When switch S is moved to this position, the cap

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Related Book For book-img-for-question

University Physics with Modern Physics

ISBN: 978-0321696861

13th edition

Authors: Hugh D. Young, Roger A. Freedman, A. Lewis Ford

See More Books

Question Posted: Sep 06, 2018 12:09 PM

See More Questions

Figure 4.9 gives a schematic representation of how the chemical potentials of the solid, liquid, and gaseous phases of a substance vary with temperature. All have a negative slope, but it is unlikely...
(a) By direct differentiation of H = U + P V, obtain a relation between (H/U)p and (U/V)p (b) Confirm that (H/U)p = I + p(V/U)p by expressing (H/U)p as the ratio of two derivatives with respect to...
With the previous problem in mind, return to Eq. (4.19) and take the origin of the coordinate system in the plane-of-incidence and on the interface (Fig. 4.47). Show that that equation is then...
The file CigaretteTax contains the state cigarette tax ($) for each state as of January 1, 2013. a. Construct an ordered array. b. Plot a percentage histogram. c. What conclusions can you reach about...
Dori Cruz started an interior design company called Interiors by Design, Inc., on April 1, 2016. The following amounts summarize the financial position of her business on April 14, 2016, after the...
Suppose a bank enters into an agreement to make a $10 million, three-year floating-rate loan to one of its best corporate customers at an initial rate of 8 percent. The bank and its customer agree to...
Larson Property Management Company is one of the largest property management companies in California, with more than 1,000 employees. The company provides a full array of commercial management and...
Are Americans superstitious? A Harris (Feb. 2013) poll of over 2,000 adult Americans was designed to answer this question. One survey item concerned the phrase "see a penny, pick it up, all day long...
How does China being Turkey's biggest import partner affect Turkey's exchange rate?
Refer to the International Journal of Retail and Distribution Management (Vol. 39, 2011) survey of Black Friday shoppers, Exercise 6.16. One question was, "How many hours do you usually spend...
In a proton accelerator used in elementary particle physics experiments, the trajectories of protons are controlled by bending magnets that produce a magnetic field of 4.80 T. What is the...
A 84.0-nF capacitor is charged to 12.0 V, then disconnected from the power supply and connected in series with a coil that has L = 0.0420 H and negligible resistance. At an instant when the charge on...
According to the Alzheimers Association (www.alz.org/documents_custom/2011_Facts_Figures_ Fact_Sheet.pdf), 3.7% of Americans with Alzheimers disease were younger than the age of 65 years in 2011...
Are all statistically significant findings meaningful? Provide a hypothetical example of a situation where a finding is statistically significant, but not substantively important. can you provide me...
Is a undecided major still acceptable these days as far as when you finish school? Do jobs accept that type of degree?
Given an unsorted array A of integers of any size, n1, and an integer value x, write an algorithm as a pseudo code (not a program!) that would find out the sum of all elements in the array that have...
can you revise this? 1. Thank you for bringing up your concerns. I understand that you may feel like your child isn't learning as much as you would like at school. However, it's important to...
Analyze the following code: What is the time complexity? int fun(int n) { int count = 0; for (int i = n; i > 0; i /= 2) for (int j=0; j
What is latency, and how does it interfere with Internet functioning?
When the concentration of a strong acid is not substantially higher than 1.0 10-7 M, the ionization of water must be taken into account in the calculation of the solution's pH. (a) Derive an...
Two irregular objects A and B carry charges of opposite sign. Figure Q21.19 shows the electric field lines near each of these objects. (a) Which object is positive, A or B? How do you know? (b) Where...
Atomic nuclei are made of protons and neutrons. This shows that there must be another kind of interaction in addition to gravitational and electric forces. Explain.
The two sides of the DNA double helix are connected by pairs of bases (adenine, thymine, cytosine, and guanine). Because of the geometric shape of these molecules, adenine bonds with thymine and...
. For each of these relations, write down all functional dependencies. If there are no functional dependencies among attributes, you must state so. Do not write down trivial functional dependencies,...
and b = 3. 7.3a=2*b 8.(5-a)*b <7 9.b
What diameter of vertical tube would allow mayonnaise (= 1,200 kg/m3) to flow under its own weight?

(a) Take first and second derivatives with respect to time of q given in Eq. (30.28), and...

Question:

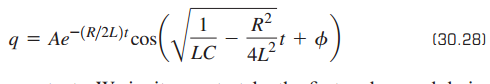
tan o and A = 2LV(1/LC) – (R²/4L²) cos o When switch S is in this position, the emf charges the capacitor. +q el When switch S is moved to this position, the capacitor discharges through the resistor and inductor.

Step by Step Answer:

Identify For part a evaluate the derivatives as sp...View the full answer

University Physics with Modern Physics

Students also viewed these Physics questions