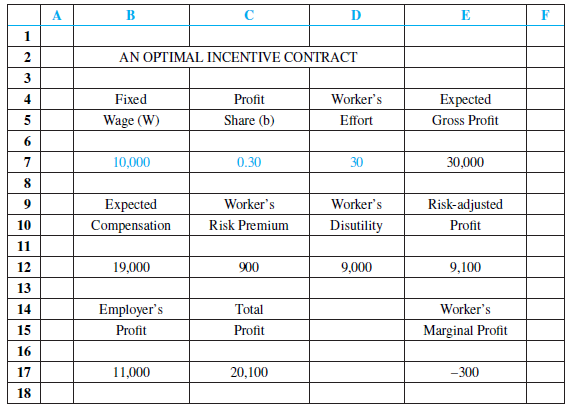
Suppose that the gross profit generated by a particular worker is given by ???? = 1,000e + u, where e denotes the worker’s effort (measured as an index between 0 and 50) and u is a random variable with a mean of zero and a positive standard deviation. Thus, profit depends not only on the worker’s effort but also on random factors beyond his control. The worker’s disutility associated with effort is given by D = 10e². The employer compensates the worker with an incentive contract of the form P = W + b????, where W is a fixed wage component and b is the worker’s profit share. For concreteness, let e = 30, and suppose that the contract calls for W = $10,000 and b = .3. Then the expected gross profit attributable to the worker is $30,000. The employer’s expected wage payment is $10,000 + (.3) ($30,000) = $19,000, and the employer’s expected profit is $30,000 − $19,000 = $11,000. In turn, the worker’s expected profit (net of any disutility) is $19,000 − 10(30)² = $10,000. Under an incentive contract, the variability in the worker’s wage (i.e., the risk) increases with the profit share b.

A risk-averse worker will discount the expected profit listed earlier by a risk premium to account for the burden of risk. To be precise, we suppose that the risk premium takes the form R = 10,000b2. The maximum premium, $10,000, occurs under 100 percent profit sharing (b = 1). Of course, for b = 0, the wage is fixed, so there is no risk and no risk premium. For b = .3, the premium is $900, so the worker’s risk-adjusted profit is $10,000 − $900 = $9,100. In general, the worker’s risk-adjusted profit is given by:

????_w = W + b(1,000e) − 10e² − 10,000b².

a. Create a spreadsheet similar to the example given. For the contract with W = $10,000 and b = .3, find the worker’s optimal level of effort.

b. Find the worker’s optimal effort levels for sharing rates of .4, .6, .8, and 1.0. What pattern do you detect?

c. Using the optimizer, find the sharing rate and level of effort that together maximize the employer and worker’s total profit.

d. If e were observable, then the parties could write a forcing contract with a fixed wage (b = 0) payable as long as the worker delivers an optimal level of effort. What level of effort maximizes total profit? Compare the total profits attained in this case with the total profits in part (c).

D AN OPTIMAL INCENTIVE CONTRACT 3 Fixed Worker's 4 Profit Expected Wage (W) Share (b) Effort Gross Profit 6. 10,000 0.30 30 30,000 Risk-adjusted Worker's Expected Compensation Worker's 10 Risk Premium Disutility Profit 11 9,100 12 19,000 900 9,000 13 14 Employer's Total Worker's Marginal Profit 15 Profit Profit 16 11,000 17 20,100 -300 18