The demand function for good X is Qdx = a + bPx + cM + e, where Px is the price of good X and M is income. Least squares regression reveals that a = 5.25, b = ?? 1.36 c = ??0.14, σa = ?? 6.19. σa = ?? 0.56, and σc = 0.05. The R-squared is 0.24.a. Compute the t-statistic for each of the estimated coefficients.b. Determine which (if any) of the estimated coefficients are statistically different from zero.c. Explain, in plain words, what the R-square in this regressionindicates.

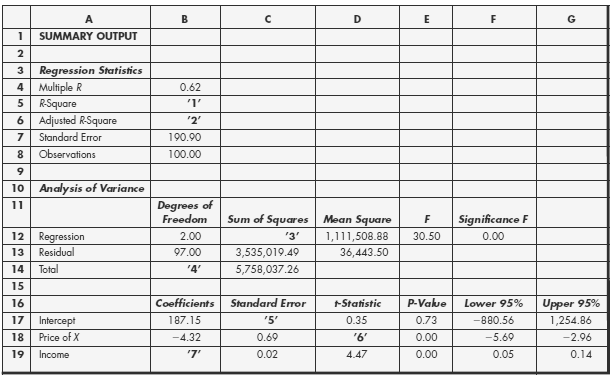
SUMMARY OUTPUT Regression Statistics Multiple R 3 0.62 4 R-Square 6 Adjusted R-Square '2' Standard Error 190.90 Observations 100.00 10 Analysis of Variance Degrees of Freedom 11 Sum of Squares Mean Square Significance F 12 Regression Residual 2.00 '3' 1,111,508.88 30.50 0.00 97.00 13 3,535,019.49 36,443.50 Total 14 '4' 5,758,037.26 15 Coefficients Standard Error P-Value Lower 95% Upper 95% 16 Statistic 17 Intercept 187.15 '5' 0.35 0.73 -880.56 1,254.86 Price of X -4.32 -5.69 18 0.69 '6' 0.00 -2.96 19 Income '7' 0.02 4.47 0.00 0.05 0.14