The formula for the price of a European call futures option in terms of the futures price, F₀, is given in Chapter 18 as

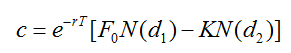
where

and K, r, T, and σ are the strike price, interest rate, time to maturity, and volatility, respectively.
(a) Prove that F₀N'(d₁) = KN'(d₂)
(b) Prove that the delta of the call price with respect to the futures price is e^-rTN(d₁).
(c) Prove that the vega of the call price is F₀ √T N'(d₁)e^-rT
(d) Prove the formula for the rho of a call futures option given in Section 19.12.
The delta, gamma, theta, and vega of a call futures option are the same as those for a call option on a stock paying dividends at rate q with q replaced by r and S₀ replaced by F₀. Explain why the same is not true of the rho of a call futures option.

Transcribed Image Text:

c = e"[F,N(d,)– KN(d,)] -rT In(F, / K)+o²T /2 oNT d, = d, -oVT