The general form for a three-dimensional stress field is given by

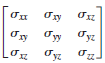
where the diagonal terms represent tensile or compressive stresses and the off-diagonal terms represent shear stresses. A stress field (in MPa) is given by

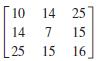
To solve for the principal stresses, it is necessary to construct the following matrix (again in MPa):

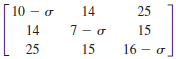
σ₁, σ₂, and σ₃ can be solved from the equation

σ³ – Iσ² + IIσ – III = 0

where

I = σ_xx + σ_yy + σ_zz

II = σ_xxσ_yy + σ_xxσ_zz + σ_yyσ_zz – σ²_xy – σ²_xz – σ²_yz

III = σ_xxσ_yyσ_zz – σ_xxσ² _yz – σ_yyσ² _xz – σ_zzσ²_{xy +} 2σ_xy σ_xz σ_yz

I, II, and III are known as the stress invariants. Find σ₁, σ₂, and σ₃ using a root-finding technique.

Om xx. Oy 10 14 25 14 7 15 25 15 16 10- 14 25 147- 15 25 1516-