The harmonic decomposition problem considered by Pisarenko can be expressed as the solution to the equation. The solution for a can be obtained by minimizing the quadratic form a*l?yya subject to the constraint that a*la = 1. The constraint can be incorporated into the performance index by means of a Lagrange multiplier. Thus the performance index becomes. By minimizing ? with respect to a, show that this formulation is equivalent to the Pisarenko eigenvalue problem given in (12.5.9) with the Lagrange multiplier playing the role of the eigenvalue. Thus show that the minimum of ? is the minimum eigenvalue ?2?.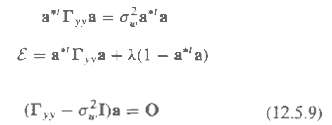

a"Ty,a = oa"a E = a"r,,a - A(1 - a"a) (12.5.9) (Ty - oDa = 0