The Levinson-Durbin algorithm described in section 11.3.1 solved the linear equations

?_ma_m?= ? ?_m

where the right-hand side of this equation has elements of the autocorrelation sequence that are also elements of the matrix ?. Let us consider the more general problem of solving the linear equations

?_mb_m = c_m

where c_m is an arbitrary vector. (The vector b_m is not related to the coefficients of the backward predictor.) Show that the solution to ?_mb_m = c_m?can be obtained from a generalized Levinson-Durbin algorithm which is given recursively as

b_m(m) = c(m) - ?^bI_{m ? 1}b_{m ? 1}/E^f_{m ? 1}

b_m(k) = b_{m ? 1}(k) ? b_m(m)a^v_{m ? 1}(m ? k)?k = 1, 2, . . . ., m ? 1

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?? m = 1, 2. . . p ?

Where b_I(1) = c(1)/?_xx(0) = c(1)/E^f₀?and a_m(k) is given by (11.3.17). Thus a second recursion is required to solve the equation ?_mb_m = c_m.

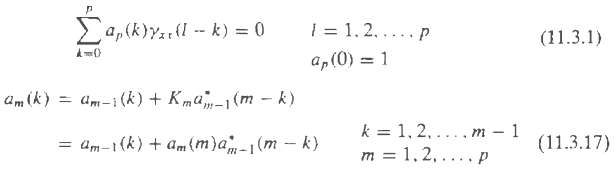
| = 1, 2. .... p La, (k)Yz:{l -- k) = 0 (11.3.1) ap(0) = 1 am (k) = am-i(k) + Kma-1 (m - k) k = 1, 2,...., m - k) = Um-1 (k) + am (m)a-1(m - (11.3.17) m = 1.2,....p