The linear system x 1 x 3 = 0.2, 1/2 x 1 + x 2

Question:

The linear system x₁ − x₃ = 0.2, −1/2 x₁ + x₂ – 1/4 x₃ = −1.425, x₁ – 1/2 x₂ + x₃ = 2. Has the solution (0.9,−0.8, 0.7)^t .

a. Is the coefficient matrix

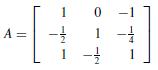
Strictly diagonally dominant?

b. Compute the spectral radius of the Gauss-Seidel matrix T_g.

c. Use the Gauss-Seidel iterative method to approximate the solution to the linear system with a tolerance of 10⁻² and a maximum of 300 iterations.

d. What happens in part (c) when the system is changed to x₁ − 2x₃ = 0.2, −1/2 x₁ + x₂ – 1/4 x₃ = −1.425, x₁ – 1/2 x₂ + x₃ = 2.

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Related Book For book-img-for-question

Numerical Analysis

ISBN: 978-0538733519

9th edition

Authors: Richard L. Burden, J. Douglas Faires

See More Books

Question Posted: Mar 22, 2016 02:57 AM

See More Questions

The linear system x 1 + 2x 2 2x 3 = 7, x 1 + x 2 + x 3 = 2, 2x 1 + 2x 2 + x 3 = 5, has the solution (1, 2,1) t . a. Show that (T j ) = 0. b. Use the Jacobi method with x (0) = 0 to approximate the...
The linear system x1 + 1/2 x2 + 1/3 x3 = 5/6, 1/2 x1 + 1/3 x2 + 1/4 x3 = 5/12, 1/3 x1 + 1/4 x2 + 1/5 x3 = 17/60
The solution by Cramers rule to the linear system a 11 x 1 + a 12 x 2 + a 13 x 3 = b 1 , a 21 x 1 + a 22 x 2 + a 23 x 3 = b 2 , a 31 x 1 + a 32 x 2 + a 33 x 3 = b 3 , has And a. Find the solution to...
The technique of performance management that establishes and monitors four dimensions of performance: Question 11Answer a. Profit, sales, productivity, and asset management performance b. Financial,...
Curleys Fried Chicken Kitchen operates two southern cooking restaurants in St. Louis, Missouri, and has the following financial structure: Accounts payable ........$ 100,000 Short-term debt ...........
Average velocity is equal to the slope of a secant line through two points on a graph. Which graph?
How would you use workforce analytics to support talent programs such as recruiting, retention, and employee development?
Oakwood Company produces maple bookcases to customer order. It received an order from a customer to produce 5,000 bookcases. The following information is available for the production of the...
The expected yield on a 2 year security is 7.8%. If the yield on a t-bill maturing in 1 year is 7.2%, what is the yield on a 1 year t-bill maturing 1 year from now?
Liz Viera has opened Pizza and More, a wholesale grocery and pizza company. The following transactions occurred in March: Required 1. Journalize the transactions. 2. Record to the accounts receivable...
Find the first two iterations of the Jacobi method for the following linear systems, using x(0) = 0: a. 3x1 x2 + x3 = 1, 3x1 + 6x2 + 2x3 = 0, 3x1 + 3x2 + 7x3 = 4. b. 10x1 x2 = 9, x1 + 10x2 2x3 =...
Repeat Exercise 11 using the Jacobi method. In Exercise 11 a. Is the coefficient matrix Strictly diagonally dominant? b. Compute the spectral radius of the Gauss-Seidel matrix T g . c. Use the...
Assuming (1) that you can buy a pound sterling call with strike price of $1.50 for 3 cents, (2) that you can sell a sterling put at the same strike price for 4 cents, (3) that the prevailing forward...
Suppose that at three units purchased, marginal utility is $8 and total utility is $30. If the marginal utility of the fourth unit purchased is $6, how much is the total utility of four units?
Each of the following is true about Walmart except that ______. a) it is the largest employer in the United States b) it is the largest company in the world c) it pays its employees, on average,...
Gas lines in the 1970s were caused by ______. a) price floors b) price ceilings c) both price floors and price ceilings d) neither price floors nor price ceilings.
Which of the following is a natural monopoly? a) the National Football League b) a local phone company c) DeBeers Diamond Company d) IBM
If a firms total revenue is $20 million, its fixed costs are $12 million, and its variable costs are $22 million, what does it do (a) in the short run and (b) in the long run?
Each bar has a mass per length of m 0 . Determine the angles and for equilibrium. The contact at A is smooth, and both are pin connected at B. A B IN
Can partitioned join be used for r r.A s? Explain your answer
Suppose the graphs of f(x) = x2 and g(x) = 2x are drawn on a coordinate grid where the unit of measurement is 1 inch. Show that, at a distance 2 ft to the right of the origin, the height of the graph...
Compare the functions f (x) = x5 and g(x) = 5x by graphing both functions in several viewing rectangles. Find all points of intersection of the graphs correct to one decimal place. Which function...
Compare the functions f (x) = x10 and g(x) = ex by graphing both f and g in several viewing rectangles. When does the graph of g finally surpass the graph of f?
Suppose the North Carolina University system tests the idea that computerization of statistics classes increases student performance in the courses. If the computers are found to have a beneficial...
M. Handy is a self-employed painter who earned $32,400 last year. Her FICA tax rate is 15.3% of her earnings. How much FICA tax did she pay?
Using the same iThe Shouldice Hospital specializes in hernia operations. They have a special procedure that not only has a much higher rate of long-term success than other hospitals, but also allows...

The linear system x 1 x 3 = 0.2, 1/2 x 1 + x 2

Question:

1 -4 A = 1 1

Step by Step Answer:

a A is not strictly diagonally dominant b Since T g is co...View the full answer

Numerical Analysis

Students also viewed these Numerical Analysis questions