The models in this section are often called combinatorial models because each solution is a combination of the various 0s and 1s, and there are only a finite number of such combinations. For the capital budgeting model in Figure 14.40, there are seven investments, so there are 27 = 128 possible solutions (some of which are infeasible). This is a fairly large number, but not too large. Solve the model without Solver by listing all 128 solutions. For each, calculate the total cash requirement and total NPV for the model. Then manually choose the one that stays within the budget and has the largest NPV.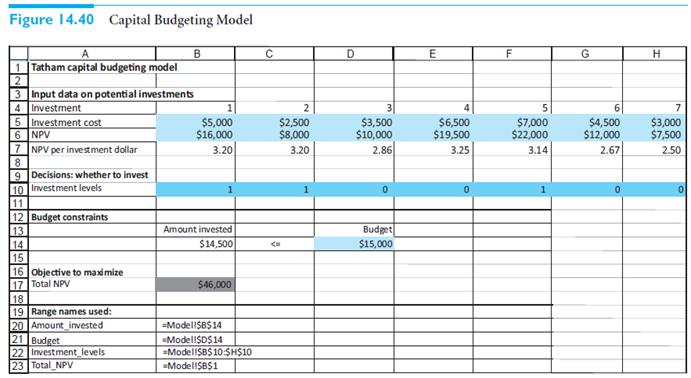

Figure 14.40 Capital Budgeting Model B D E 1 Tatham capital budgeting model 2 3 Input data on potential investments 4 Investment 5 Investment cost 6 NPV 7 NPV per investment dollar 8. 9 Decisions: whether to invest 10 Investment levels 11 12 Budget constraints 13 14 15 16 Objective to maximize 17 Total NPV 3 $3,500 $10,000 2.86 2 5 6. $5,000 $16,000 3.20 $2,500 $8,000 $6,500 $19,500 $7,000 $2,000 $4,500 $12,000 2.67 $3,000 $7,500 3.20 3.25 3.14 2.50 Amount invested Budget $15,000 $14,500 $46,000 18 19 Range names used: 20 Amount_ ivested 21 Budget 22 Investment_levels 23 Total_NPV =Modeli$B$14 ModellSD$14 =ModellSB$10:SH$10 =Modell$B$1