Question: The Rao-Hartley-Cochran (1962) method for selecting psus with unequal probabilities. To take a sample of size n, divide the population into n random groups of

The Rao-Hartley-Cochran (1962) method for selecting psus with unequal probabilities. To take a sample of size n, divide the population into n random groups of psus, U₁, U₂, . . . ,U_n. Then select one psu from each group with probability proportional to size. Let Nk be the number of psus in group k. If psu i is in group k, it is selected with probability xki = M_i / Ʃ_j_{∈Uk Mj} ; the estimator is

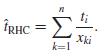
RHC Xki !

Show that ṫ_RHC is unbiased for t, and find its variance. Use two sets of indicator variables. Let I_ki = 1 if psu i is in group k and 0 otherwise, and let Z_i = 1 if psu i is selected to be in the sample.

RHC Xki !

Step by Step Solution

★★★★★

3.53 Rating (174 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Sing the indicator variables And We show that RHC is conditionally unbiased for t given the grouping ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Document Format (1 attachment)

627-M-S-S-D (2473).docx

120 KBs Word File

Students Have Also Explored These Related Statistics Questions!

It costs you $10 to draw a sample of size n = 1 and measure the attribute of interest. You have a budget of $1,500. a. Do you have sufficient funds to estimate the population mean for the attribute...

It costs you $10 to draw a sample of size n = 1 and measure the attribute of interest. You have a budget of $1,200. a. Do you have sufficient funds to estimate the population mean for the attribute...

A random sample of size n is drawn without replacement from an urn containing r red chips and w white chips. Define the random variable X to be the number of red chips in the sample. Use the...

The Rao-Hartley-Cochran (1962) method for selecting psus with unequal probabilities. To take a sample of size n, divide the population into n random groups of psus, U1, U2, . . . ,Un. Then select one...

It is a three-part discussion that should be completed in sequential order. Part One - Hypothesis Testing ReadLecture Four. Lecture Four starts out with the five-step procedure for hypothesis...

1. Calculate the sample size needed given these factors: one-tailed t-test with two independent groups of equal size small effect size (see Piasta, S.B., & Justice, L.M., 2010) alpha =.05 beta = .2...

\fThis is an electronic version of the print textbook. Due to electronic rights restrictions, some third party content may be suppressed. Editorial review has deemed that any suppressed content does...

SAMPLING MEAN: DEFINITION: The term sampling mean is a statistical term used to describe the properties of statistical distributions. In statistical terms, the sample mean from a group of...

The Ahoy Manufacturing Company in Rochester, Minnesota, assembles and tests electronic components used in smartphones. Consider the following data regarding component T24 (amounts are per unit):...

Design an ER diagram that shows the main tables used in a pharmacy. The tables are Patient, Drug, Prescription, Doctor, and Vendor. Show in the ER diagram the main entities with their attributes as...

2 0 - 1 0 . Legacy Enterprises received an invoice from its supplier. The terms of credit were stated as 3 / 1 5 , n 4 5 . Calculate the effective annual interest rate on the trade credit.

2. What four benefits do owners of common stock usually enjoy?

Suppose the age distribution in a city is as follows. Under 18 ...... 22% 1825 ......... 18% 2650 ......... 36% 5165 ......... 10% Over 65 ....... 14% A researcher is conducting proportionate...

Candidate Jones believes she will receive .55 of the total votes cast in her county. However, in an attempt to validate this figure, her pollster contacts a random sample of 600 registered voters in...

Determine a possible frame for conducting random sampling in each of the following studies. a. The average amount of overtime per week for production workers in a plastics company in Pennsylvania b....

9 53% of students entering four-year colleges receive a degree within six years. Is this percent smaller than for students who play intramural sports? 122 of the 235 students who played intramural...

Muller's Investigative Services has stock is trading at $65 per share. The stock is expected to have a year-end dividend of $4 per share (D1 = $4), and it is expected to grow at some constant rate,...

An investor is considering a portfolio consisting of investment in three securities 1, 2, and 3. The means and standard deviations of expected returns for the three individual securities are:...