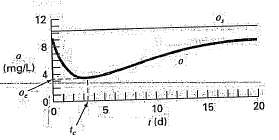
The Streeter-Phelps model can be used to compute the dissolved oxygen concentration in a river below a point discharge of sewage (Figure),

o = o_s?? k_dL_o/k_d + k_s ? k_a (e^?kat?? e^{?(kd + ks)t}) ? S_b/k_a?(1 ? e^?kat)

where o = dissolved oxygen concentration [mg/L], o_s = oxygen saturation concentration [mg/L], t = travel time [d], L_o = biochemical oxygen demand (BOD) concentration at the mixing point [mg/L], k_d = rate of decomposition of BOD [d^-1], k_s = rate of setting of BOD [d^-1], k_a = reaeration rate [d^-1], and S_b = sediment oxygen demand [mg/L/d]. As indicated in Figure. Eq (P16.16) produces an oxygen ?sag? that reaches a critical minimum level o_c some travel time t_c below the point discharge. This point is called ?critical? because it represents the location where biota that depend on oxygen (like fish) would be the most stressed. Determine the critical travel time and concentration, given the following values:

o_s = 10 mg/L? ?? ? ? ? ? ??k_d = 0.2 d^?1? ? ??? ? ? ? ? ??k_a = 0.8 d^?1

?k_s = 0.06 d^?1 ?? ? ? ? ? ??L_o = 50 mg/L? ?? ? ? ? ? ??S_b = 1 mg/L/d

12 (mg/L) 20 15 10 5.