The top shown is supported at the fixed point O. Denoting by , , and the Eulerian angles defining the position of the

The top shown is supported at the fixed point O. Denoting by φ , θ, and ψ the Eulerian angles defining the position of the top with respect to a fixed frame of reference, consider the general motion of the top in which all Eulerian angles vary.

(a) Observing that ΣMZ = 0 and 0, ΣMZ = and denoting by I and I??, respectively, the moments of inertia of the top about its axis of symmetry and about a transverse axis through O, derive the two first order differential equations of motion where α and β are constants depending upon the initial conditions. These equations express that the angular momentum of the top is conserved about both the Z and z axes, that is, that the rectangular component of H0 along each of these axes is constant.

(b) Use Eqs (1) and (2) to show that the rectangular component ωz of the angular velocity of the top is constant and that the rate of precession φ depends upon the value of the angle of notation θ.

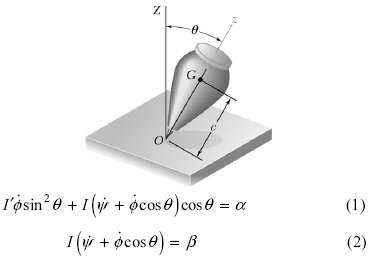
Z I'osin0 + 1 (y + ocos) cos = a 1 (v + cose) = B (1) (2)