The unexplained variation for Model 1 of the previous exercise is .3936. If we set both 5 and 6 in this model equal to 0

The unexplained variation for Model 1 of the previous exercise

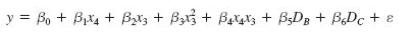
is .3936. If we set both β5 and β6 in this model equal to 0 (that is, if we eliminate the dummy variable portion of this model), the resulting reduced model has an unexplained variation of 1.0644. Using an α of .05, perform a partial F- test (see page 573) of H0: β5 = β6 = 0. If we reject H0, we conclude that at least two of advertising campaigns A, B, and C have different effects on mean demand. Many statisticians believe that rejection of H 0 by using the partial F- test makes it more legitimate to make pairwise comparisons of advertising campaigns A, B, and C, as we did in part a of the previous exercise. Here, the partial F- test is regarded as a preliminary test of significance.

y = Bo + B4 + Bx3 + Ba + Bz + B;DB + BeDc + e %3D