Question: There are two types of consumers 1 and 2 with demands: P 1 (Q) = a b 1 Q P 2 (Q) = a

There are two types of consumers 1 and 2 with demands:

P₁(Q) = a – b₁Q

P₂(Q) = a – b₂Q

The monopolist has a marginal cost function given by

MC(Q)

a. Shows that if there is no price discrimination, then the profit maximizing price and quantity, (P*, Q*), satisfy

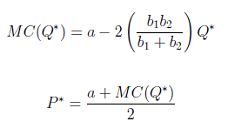
bib2 2(5+ b3) MC(Q') = a – 2 Q* bị + b2 a + MC(Q*) 2 P*:

b. Under third degree price discrimination, let (P₁, Q₁) and (P₂, Q₂) be the profit maximizing prices and quantities for consumers 1 and 2, respectively. Show that:

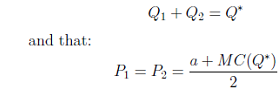
bib2 2(5+ b3) MC(Q') = a 2 Q* b + b2 a

That is, under this particular kind of demand system a monopolist that can practice third degree price discrimination will not benefit from doing so. It will choose prices that are the same for both customers and equal to the price level under no price discrimination.

bib2 2(5+ b3) MC(Q') = a 2 Q* b + b2 a + MC(Q*) 2 P*:

Step by Step Solution

★★★★★

3.44 Rating (170 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

a Without PD P 1 P 2 P Total Q a Pb 1 aPb 2 P a b 1 b 2 b 1 b ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Document Format (1 attachment)

68-B-F-F-M (2256).docx

120 KBs Word File

Students Have Also Explored These Related Finance Questions!

What was Oaktree's strategy for investing in CIT's publicly traded debt? Compute the return on investment for Oaktree if CIT files for bankruptcy now. (Historical recovery rates for senior secured...

There are two types of electric pencil-sharpener producers. High-quality manufacturers produce very good sharpeners that consumers value at $14. Low-quality manufacturers produce less good ones that...

Two identical buggies 1 and 2 with one man in each move without friction due to inertia along the parallel rails toward each other. When the buggies get opposite each other, the men exchange their...

There are two types of professional wrestlers: "babyfaces" ("good guys") and "heels" ("bad guys"). Between any pair of professional wrestlers, there may or may not be a rivalry. Suppose we have n...

A monopolist sells health insurance to two types of consumers, "1" and "2". Type "1" is less healthy than type "2", such that the marginal cost of providing health services for type "1" is greater...

The equation for line r can be written as y = 4 -Ax - 2. Line s is perpendicular to line r and 9 passes through (3, 5). What is the equation of line s?

In 2019, the U.S. Business Roundtable redefined the purpose of corporations away from maximizing shareholder value to "promoting an economy that serves all stakeholders which include customers,...

Consider a monopoly with marginal cost equal to 4. There are two types of customers: high type (H) with demand p = 20 - Q and low type (L) with demand p = 16 - Q. a. Assume the monopoly can observe...

Consider a monopolist selling sweets to two types of consumers (assume sweets are innitely divisible, so that the monopolist can sell any nonnegative quantity). The demand of consumers of type 1 is...

Find an expression for the derivative of cosech1x in terms of x

When stock is exchanged for stock in a business combination, how is the stock exchange ratio generally expressed?

What manufacturing process would you recommend to produce a large quantity of the following parts while minimizing cost? ( a ) automotive door panel where structural performance is not critical but...

Tell whether each of the following transactions related to an office building is a revenue expenditure (RE) or a capital expenditure (CE). In addition, indicate whether each transaction is an...

Santana Rey, owner of Business Solutions, decides to prepare a statement of cash flows for her business. Required Prepare a statement of cash flows for Business Solutions using the indirect method...

Find the points on the ellipse 4x2 + y2 = 4 that are farthest away from the point (1, 0).

Six equal annual contributions are made to a fund, with the first deposit on December 31, 2007. Required Using the future value tables, determine the equal contributions that, if invested at 10%...

Bigbox, Inc. has bonds outstanding that will mature in eight years. These bonds pay interest semiannually and have a coupon rate of 4.6 percent. If the bonds are currently selling at $888.92, what is...

36. Newsboy calculator Design a spreadsheet to calculate the optimal order-up-to point for a newsboy problem with normally distributed demands. In order to avoid table look-ups, use the approximation...

Profits have been decreasing for several years at Pegasus Airlines. In an effort to improve the companys performance, consideration is being given to dropping several flights that appear to be...

Birch Company normally produces and sells 30,000 units of RG-6 each month. RG-6 is a small electrical relay used as a component part in the automotive industry. The selling price is $22 per unit,...

Jackson County Senior Services is a nonprofit organization devoted to providing essential services to seniors who live in their own homes within the Jackson County area. Three services are provided...

Estimate a multiple linear regression relationship with the U.K. stock returns as the dependent variable, and U.K. Government Bond yield (Interest rate), U.S. Stock Returns, and Japan Stock Returns...

A machine that cost $ 1 2 0 , 0 0 0 3 years ago can be sold now for $ 5 2 , 7 5 0 . Its market value is expected to be $ 4 0 , 0 0 0 and $ 2 0 , 0 0 0 1 year and 2 years from now, respectively. Its...

Answer using JASP Software, etc. Is there a difference in profit in the first quarter compared to the second quarter for investor's portfolios? Each participant's investment portfolio was evaluated...