This exercise will lead you through a proof of Chebyshev’s inequality. Let X be a continuous random variable with probability density function f (x). Suppose that P(X

a. Show that

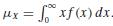
b. Let k >0 be a constant. Show that μ_X ≥

c. Use part (b) to show that P(X ≥ k) ≤ μ_X /k. This is called Markov’s inequality. It is true for discrete as well as for continuous random variables.

d. Let Y be any random variable with mean μ_Y and variance σ²_Y. Let X = (Y − μ_Y)². Show that μ_X = σ²_Y.

e. Let k > 0 be a constant. Show that P(|Y −μ_Y| ≥ kσ_Y ) = P(X ≥ k²σ²_Y).

f. Use part (e) along with Markov’s inequality to prove Chebyshev’s inequality: P(|Y − μ_Y| ≥ kσ_Y ) ≤ 1/k².

Hy = 10 xf(x) dx kf(x)dx = k P (X > k).