A bead is released from rest at the origin and slides down a frictionless wire that connects the origin to a given point, as shown in Fig. You wish to shape the wire so that the bead reaches the endpoint in the shortest possible time. Let the desired curve be described by the function y(x), with downward taken to be positive. Show that y(x) satisfies where C is a constant. Show that x and y may be written as.

This is the parametrization of a cycloid, which is the path taken by a point on the edge of a rolling wheel.

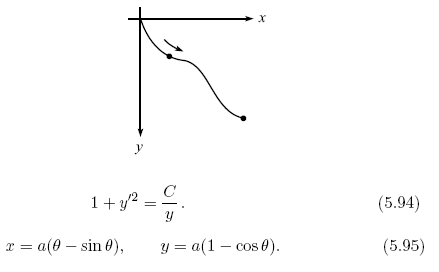
1+y/2 (5.94) y = a(1 cos 0). r = a(0 sin 0), (5.95)