(a) Generalize the circumstances of the collision of Problem 14.5 to nonzero angular momentum (impact parameter) and...
Question:
(a) Generalize the circumstances of the collision of Problem 14.5 to nonzero angular momentum (impact parameter) and show that the total energy radiated is given by
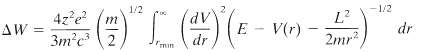
where rmin is the closest distance of approach (root of E ? V ? L2/2mr2), L = mbv0, where b is the impact parameter, and v0 is the incident speed (E = mv20/2).
(b) Specialize to a repulsive Coulomb potential V(r) = zZe2/r. Show that ?W can be written in terms of impact parameter as
where t = bmv20/zZe2 is the ratio of twice the impact parameter to the distance of closest approach in a head-on collision. Show that in the limit of t going to zero the result of Problem 14.5b is recovered, while for t >> 1 one obtains the approximate result of Problem 14.7a.
(c) Using the relation between the scattering angle 0 and t (= cot ?/2), show that ?W can be expressed as
(d) What changes occur for an attractive Coulomb potential?
Step by Step Answer:
a However this can be converted to an integral over the trajectory By s...View the full answer
