Question: Suppose thal we wish to extend the method described for finding one generalized eigenvector to finding two (or more) generalized eigenvectors. Let's look at the
Suppose thal we wish to extend the method described for finding one generalized eigenvector to finding two (or more) generalized eigenvectors. Let's look at the case where 
has multiplicity 3 but has only one linearly independent eigenvector io. First. we find 
1 by the method described in this section. Then we find 
2 such that
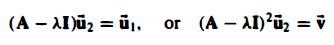
(We continue in this fashion to obtain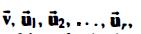
for r and r is the number of "missing" eigenvectors for 
.)
(a) Show that
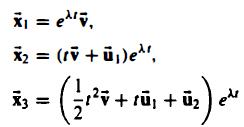
are solutions of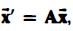
given that 
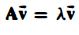and 
has multiplicity 3 and r = 2.
(b) Show that the vectorsv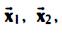
and 
are linearly independent.
(c) Solve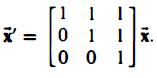 
(A AI)z = j. or (A AI)z = v
Step by Step Solution
3.55 Rating (159 Votes )
There are 3 Steps involved in it
a i ii iii b We first show that the set is linearly independent i Observe that from the definitions ... View full answer
Get step-by-step solutions from verified subject matter experts
Document Format (1 attachment)
947-M-L-A-L-S (4983).docx
120 KBs Word File
Study Help