(a) Show that the Green function G(x, y; x', y?) appropriate for Dirichlet boundary conditions for a square two-dimensional region, 0 ? x ? l, 0 ? y ? l, has an expansion

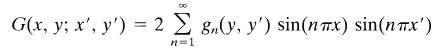
Where g_n(y, ?y?) satisfies

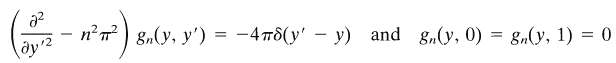
(b) Taking for g_n(y, y') appropriate linear combinations of sinh(n?y') and cosh(n?y') in the two regions, ?' ?, in accord with the boundary conditions and the discontinuity in slope required by the source delta function, show that the explicit form of G is

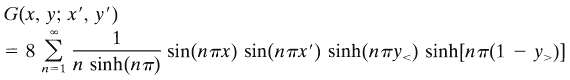
Where y_{(y>) is the smaller (larger) of ? and y'.}

G(x, y; x', y') = 2 2 8,(y, y') sin(n Tx) sin(nTx') n=1