Consider a potential problem in the half-space defined by z ? 0, with Dirichlet boundary conditions on
Question:
Consider a potential problem in the half-space defined by z ? 0, with Dirichlet boundary conditions on the plane z = 0 (and at infinity).
(a) Write down the appropriate Green function G(x, x').
(b) If the potential on the plane z = 0 is specified to be ? = V inside a circle of radius a centered at the origin, and ? = 0 outside that circle, find an integral expression for the potential at the point P specified in terms of cylindrical coordinates (p, ?, z).
(c) Show that, along the axis of the circle (p = 0), the potential is given by
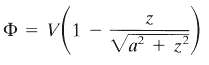
(d) Show that at large distances (p2 + z2 >> a2) the potential can be expanded in a power series in (p2 + z2)-1 and that the leading terms
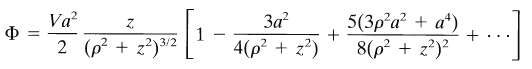
Verify that the results of parts с and d are consistent with each other in their common range ofvalidity.
Step by Step Answer:
a The Green function The Green function for a half space z 0 with Dirichlet boundar...View the full answer
