(a) Show that the quadrupole term in the multi pole expansion can be written where here is the Kronecker delta, and Qij is the quadrupole moment of the charge distribution. Notice the hierarchy: The monopole moment (Q) is a scalar, the dipole moment (p) is a vector, the quadrupole moment (Qij) is a second-rank tensor, and so on.

(b) Find all nine components of Qij for the configuration in Fig. 3.30 (assume the square has side a and lies in the xy plane, centered at the origin).

(c) Show that the quadrupole moment is independent of origin if the monopole and dipole moments both vanish. (This works all the way up the hierarchy--the lowest nonzero multi pole moment is always independent of origin.)

(d) How would you define the octopole moment? Express the octopole term in the multi pole expansion in terms of the octopole moment.

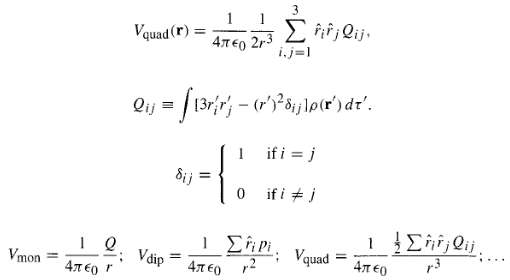
Vmon | 0 Vquad (r) Vdip 2j = f13r{r} - Gr'338yj\pr')dt'. if i = j So if it i dij 1 1 2,3 = i,j=1 1 i Vquad 1..