Regarding the converse stated in Exercise 6, if the events A_n,n ≥ 1, are not independent, then P(lim sup_n→∞ A_n) = 0 need not imply that 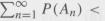∞. Give one or two concrete examples to demonstrate this assertion. Take (Ω, A, P) = ((0, 1), B_(0,1), λ),λ being the Lebesgue measure. Then

(a) Take

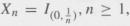
and show that

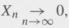
so that

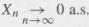
Then, by Exercise 5, P(lim sup_n→∞, A_n) = 0, where A_n = (|X_n| ≥ l/k) for any arbitrary but fixed k = 1, 2,... Also, show that

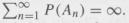
(b) Take

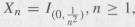
and show that

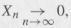
so that

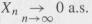
Again, P(lim sup _n→∞ A_n) = = , as in (a). Also show that

P(A_n)

2n=1 P(A,)