Question: All sets figuring below are subsets of the product space W 1 ´ W 2 . Then show that (i) E Ã F implies E

All sets figuring below are subsets of the product space W1´ W2. Then show that

(i) E Í F implies Ew1 Í Ew1 and Ew2 Ã Ew2, w1 ÃŽ W1, w2 ÃŽ, W2.

(ii) E Ç F Ø implies Ew1 Ã‡Ew1 = Ew2 Ã‡ Ew2 = Ø, w1 ÃŽ W1, w2 ÃŽ W2.

(iii) For n = 1, 2,€¦.

= U En,02 n = 1, 2, ..., (U En = U En,01, (U En 02

And in particular,

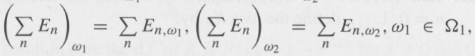
All sets figuring below are subsets of the product space

w2 ÃŽ W2.

(iv) For n = 1, 2,€¦.,

All sets figuring below are subsets of the product space

w2 ÃŽ W2.

(v) (Ec) w1 = (Ew1)c, (Ec) w2 = (Ew2)c, w1 ÃŽ W1, w2 ÃŽ W2.

= U En,02 n = 1, 2, ..., (U En = U En,01, (U En 02

Step by Step Solution

★★★★★

3.49 Rating (179 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

i 2 E 1 implies that 1 2 E so that 1 2 F and then 2 F 1 Thus E 1 F 1 Similarly E 2 F 2 ii If E 1 F 1 ... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Document Format (1 attachment)

Word file Icon

742-M-S-P (6864).docx

120 KBs Word File

Students Have Also Explored These Related Statistics Questions!

Q:

For the given sets A and B, find A B, A B, and Ac (the complement of A). 1. A and B are subsets of the set S = {0, 1, 2, 3, 4}. A = {0, 1, 2} and B = {0, 2, 4}. 2. A and B are subsets of the set S...

Q:

1. Let S = {1, 3, 5, 7} and T = {2, 5, 7}. Give an example of a subset of T that is not a subset of S. 2. Suppose that S and T are subsets of the set U. Under what circumstance will S T = T? 3....

Q:

1. What is the relationship between the two sets A and B if A B = ? 2. What is the relationship between the two sets A and B if n (A B) = n (A) + n (B)? 3. Suppose that A and B are subsets of the...

Q:

Chapter 7 The Binomial Model In this chapter, we construct the geometric binomial model for stock price movement and use the model to determine the value of a general European claim. An important...

Q:

4 This assignment, based on the content of Unit 4 of the Study Guide, is worth 3% of your grade. We recommend that you hand it in after you complete Unit 4. You must show all of your work in order to...

Q:

Give Correct ANSWERS Human-Computer Interaction (a) If you had been one of the original inventors of the WIMP interface, and engineers on the technical team had been sceptical about the advantages...

Q:

Answer the questions. in the following attachments. Question 1. (10 marks) Consider the function z = f(x, y) = x/y. Showing all steps, use the Newton Quotient approach to find ?z/?y. Question 2. (5...

Q:

Each separate response must have approximately 200 words. Assignments vary widely; however, essays should be written in APA style, with in-text citations and a separate reference listing as...

Q:

Each separate response must have approximately 200 words. Assignments vary widely; however, essays should be written in APA style, with in-text citations and a separate reference listing as...

Q:

Each separate response must have approximately 200 words. Assignments vary widely; however, essays should be written in APA style, with in-text citations and a separate reference listing as...

Q:

Rein Inc. reported deferred tax assets and deferred tax liabilities at the end of year 1 and at the end of year 2. For the year ended 12/31/Y2, Rein should report deferred income tax expense or...

Q:

A positive point charge is at a distance R/2 from the center of an uncharged thin conducting spherical shell of radius R. Sketch the electric field lines set up by this arrangement both inside and...

Q:

What is the initial goodwill related to this acquisition? Select one: a . $ 5 2 , 0 0 0 b . $ 1 8 , 3 0 0 c . $ 3 6 , 0 0 0 d . $ 3 1 , 0 0 0

Q:

If there were 16 people on the project, and that number increases to 25, which of the following must also be true? A. The development of the communications management plan will be more difficult. B....

Q:

The Wayne Manufacturing Company purchases a certain part from suppliers A, B, and C. Supplier A supplies 60% of the parts, B 30%, and C 10%. The quality of parts varies among the suppliers, with A,...

Q:

The Wayne Manufacturing Company purchases a certain part from suppliers A, B, and C. Supplier A supplies 60% of the parts, B 30%, and C 10%. The quality of parts varies among the suppliers, with A,...

Q:

Bayes theorem and conditional probability can be used in medical diagnosis. Prior probabilities of diseases are based on the physicians assessment of factors such as geographic location, seasonal...

Q:

An investor has short-short stock ABC and has to give them back in 4 month time. Against adverse evolution of ABC price this investor hedges his position with future contract based on ABC maturing in...

Q:

Suppose you have a health insurance plan with... . $2,000 deductible . 30% coinsurance $8,000 out-of-pocket maximum For a surgery that costs $17,000, what will you end up paying out-of-pocket? Note:...

Q:

Aday Acoustics, Inc., projects unit sales for a new seven-octave voice emulation implant as follows: Year Unit Sales 1 80,000 2 93,000 3 107,000 4 102,000 5 83,000 Production of the implants will...