Question: By use the expression for the fourth joint moment for Gaussian random variables, show that Under the condition that the sequence x(n) is a zero-mean

By use the expression for the fourth joint moment for Gaussian random variables, show that Under the condition that the sequence x(n) is a zero-mean white Gaussian noise sequence with variance ?2x.

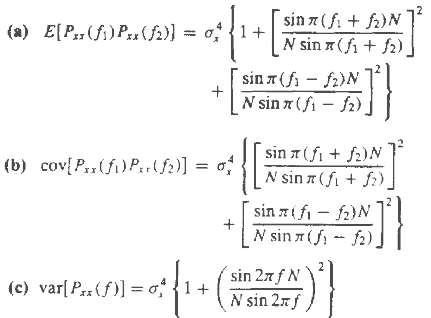
sin 7 (fi + f)N 1 + N sin (fi + f2)

sin 7 (fi + f)N 1 + N sin (fi + f2) (a) E[P,(fi) P()) = 0 sin 7 (fi - fi)N N sin x (fi - f2) sin 7 (fi + f2)N N sin 7 (fi + f) (b) cov{P(fi) P..()] = o; sin 7(f-f)N N sin 7(f - f2) sin 27f N N sin 27f (c) var[ Pz(f)] = o1+

Step by Step Solution

★★★★★

3.35 Rating (161 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

a b c Ezzmyr1m N... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Document Format (1 attachment)

31-E-T-E-D-S-P (959).docx

120 KBs Word File

Students Have Also Explored These Related Telecommunication Engineering Questions!

Use the expression for excess burden EBx= (.5pxxtx2 )/(1/ +1/) (where is the absolute value of the compensated price elasticity of demand and is the supply elasticity) to estimate the annual excess...

Use the expression for the magnetic field of a loop to find an expression for the magnitude of the magnetic field at point P, a distance a/2 from the center of each coil Note that there is a total of...

A Gaussian random variable with zero mean and variance 2X is applied to a device that has only two possible outputs, 0 or 1. The output 0 occurs when the input is negative, and the output 1 occurs...

1. A player throws a fair die and simultaneously flips a fair coin. If the coin lands heads, then she wins twice, and if tails, then one-half of the value that appears on the die. Determine her...

The number of traffic accidents that occur on a particular stretch of road during a month follows a Poisson distribution with a mean of 7.6. Find the probability that less than three accidents will...

Question: Show that it is undecidable, given the source code of a program Q, to tell whether or not any of the following is true: (i) Q halts on input 0. (ii) Q is total - that is, Q(y) halts for all...

ENGI-5132-WA Digital Communication Systems Dr. Salama Ikki, Homework Set 2 Problem 1 A coin is ipped three times and the random variable X denotes the total number of heads that show up. The...

1) Suppose X ~ N130, 25 . Find; a) P(X 140) b) P(X 120) c) P(130 X 135) 2) The random variable X is normally distributed with mean 500 and standard deviation 100. Find; (i) P(X 400) , (ii) P(X 620)...

Given: . Probability Density Function (PDF): 0(1 -2)0-1 if0 0 is an unknown parameter. Based on these observations, determine an estimate of & using (a) maximum likelihood (b) method of moments 2....

(a) Find the slope of the tangent line to the polar curve r = 2sin -3cos+1 at = /4 (b) Find an equation of the parabola that is symmetric about the x-axis, has its vertex at the origin and passes...

How many of the following functions are anti derivatives of f(x) = x -2x +4? (i) F(x) = - (x +1) +3x +9, (ii) F(x) = 13x - x + 4x +1, (ii) F3(x) = 2x - 4, (iv) F4(x)=x-(2-x) + 1, (v) F5(x) = x + (x -...

3. Joseph A. Bank often has a deal in which men can buy one suit and get two free. The file Banks.xlsx contains the valuations of 50 representative customers for one, two, or three suits. Suppose it...

How much work is required to stop an electron (m = 9.11 x 10-31 kg) which is moving with a speed of 1.90 x 106 m/s?

A rocket is fired straight up, burning fuel at the constant rate of kilograms per second. Let v = v(t) be the velocity of the rocket at time and suppose that the velocity of the exhaust gas is...

A triangle with area 30cm2 is cut from a corner of a square with side 10 cm, as shown in the figure. If the centroid of the remaining region is 4 cm from the right side of the square, how far is it...

A dog sees a rabbit running in a straight line across an open field and gives chase. In a rectangular coordinate system (as shown in the figure), assume: (i) The rabbit is at the origin and the dog...

The conditional probability distribution of Y given X = x is FY|X(y) = XExy for y > 0 and the marginal probability distribution of X is a continuous uniform distribution over 0 to 10. (a) Graph is...

2 Edgar uses the cash method to report the income from his software consulting business. A large publicly held corporation has offered to invest in Edgars business as a limited partner. What tax...

The table gives data concerning the shrink fit of two cylinders of differing materials and dimensional specification in inches. Elastic constants for different materials may be found in Table A5....

Force fits of a shaft and gear are assembled in an air-operated arbor press. An estimate of assembly force and torque capacity of the fit is needed. Assume the coefficient of friction is f, the fit...

A utility hook was formed from a 1-in-diameter round rod into the geometry shown in the figure. What are the stresses at the inner and outer surfaces at section A-A if the load F is 1000 lbf? in 10...

If the interest rates on all bonds rise from 5 to 6 percent over the course of the year, which bond would you prefer to have been holding? Consider a one - year holding period. A bond with twenty...

Problem 4-25 Complete cosh budget [LO4-2] Harry's Carryout Stores has eight locations The firm wishes to expand by two more stores and needs a bank loan to do this Mr Wilson, the banket will finance...

Question 12 Use PMT = to determine the regular payment amount, rounded to the nearest dollar. The price of a home is $300,000. The bank requires a 20% down payment. After the down payment, the...