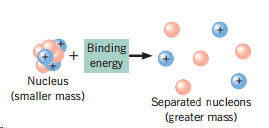
Question: (a) Energy is required to separate a nucleus into its constituent nucleons, as Figure 31.3 indicates; this energy is the total binding energy of the
(a) Energy is required to separate a nucleus into its constituent nucleons, as Figure 31.3 indicates; this energy is the total binding energy of the nucleus. In a similar way one can speak of the energy that binds a single nucleon to the remainder of the nucleus. For example, separating nitrogen ![]() into nitrogen
into nitrogen ![]() and a neutron takes energy equal to the binding energy of the neutron, as shown below:
and a neutron takes energy equal to the binding energy of the neutron, as shown below:
Figure:
![]()
Find the energy (in MeV) that binds the neutron to the ![]() nucleus by considering the mass of
nucleus by considering the mass of ![]() (atomic mass = 13.005 738 u) and the mass of
(atomic mass = 13.005 738 u) and the mass of ![]() (atomic mass = 1.008 665 u), as compared to the mass of
(atomic mass = 1.008 665 u), as compared to the mass of ![]() (atomic mass = 14.003 074 u).
(atomic mass = 14.003 074 u).
(b) Similarly, one can speak of the energy that binds a single proton to the ![]() nucleus:
nucleus:
![]()
Following the procedure outlined in part (a), determine the energy (in MeV) that binds the proton (atomic mass = 1.007 825 u) to the ![]() nucleus. The atomic mass of carbon
nucleus. The atomic mass of carbon ![]() is 13.003 355 u.
is 13.003 355 u.
(c) Which nucleon is more tightly bound, the neutron or the proton?
14 N EnergyN+on 4N
Step by Step Solution
3.33 Rating (156 Votes )
There are 3 Steps involved in it
a The mass defect is m 13005 738 u 1008 665 u 14003 074 u 0011 329 u ... View full answer

Get step-by-step solutions from verified subject matter experts
Document Format (1 attachment)
1176-P-M-P-A-S(1621).docx
120 KBs Word File


