Question: Computation of the even and odd harmonics using the DFT Let x(n) be an N-point sequence with an n-point DFT X(k) (N even) (a) Consider

Computation of the even and odd harmonics using the DFT Let x(n) be an N-point sequence with an n-point DFT X(k) (N even)

(a) Consider the time-aliased sequence. What is the relationship between the M-point DFT Y(k) of y(n) and the Fourier transform X(?) of x(n)?

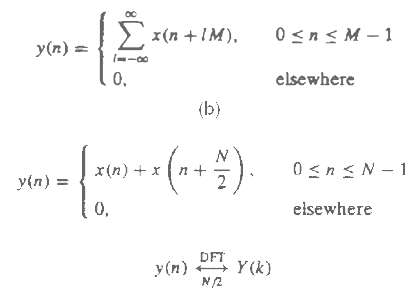
x(n +IM). 0

(b) Let, and show that X(k) = Y(k/2), k = 2, 4, . . . , N ? 2?

(c) Use the results in parts (a) and (b) to develop a produce that computes the odd harmonics of X(k) using an N/2-point DFT.

x(n +IM). 0

Step by Step Solution

★★★★★

3.41 Rating (164 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

a b c Yk No... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Document Format (1 attachment)

Word file Icon

31-E-T-E-D-S-P (767).docx

120 KBs Word File

Students Have Also Explored These Related Telecommunication Engineering Questions!

Q:

What is the relationship between tuition and student enrollment at a university. How would this relationship be graphed?

Q:

What is the relationship between FIFO and clock page replacement algorithms?

Q:

What is the relationship between the firms target capital structure and the weighted average cost of capital (WACC)?

Q:

(11) A bandpass filter is needed to recover x2(n) from the signal, x(n) = x1(n) + X2(n) + x3(n), where x1 (n) = sin(.5n), X2(n) = sin(1.4n), and X3(n) = cos(2.7n). (a) Give specific cut-off...

Q:

s sf Define the terms opaque type and concrete type. [5 marks] The following is a shortened version of one of the definition modules described in the Modula-2 user manual: Provide a suitable...

Q:

Consider the computation of the autocorrelation estimate where x[n] is a real sequence. Since ? xx [?m] = ? xx [m], it is necessary onlu to evaluate Eq. (p10.38-1) for 0 ? m ? M ? 1 to obrain ? xx...

Q:

# 5: Fourier Interpolant and DFT 1 The Discrete Fourier Transform (DFT) of a periodic array fj , for j = 0, 1, . . . , N 1 (corresponding to data at equally spaced points, starting at the left end...

Q:

Consider the following procedure? (a) Form the sequence v[n] = x 2 [2n] where x 2 [n] is given by Eq. (8.166). This yields? v[n] = x[2n]? ? ? ? ? ? ? ? ? n = 0, 1 ?. N/2 ? 1 v[N ? 1 ? n] = x[2n +...

Q:

DFI of real sequences with odd harmonics only Let x(n) be an N -point real sequence with N-point DFT X(k) (N even). In addition, x(n) satisfied the following symmetry property: x(n + N/2) = -x(n) n =...

Q:

# 5: Fourier Interpolant and DFT 1 The Discrete Fourier Transform (DFT) of a periodic array fj , for j = 0, 1, . . . , N 1 (corresponding to data at equally spaced points, starting at the left end...

Q:

Two trucks of equal mass collide at a 90 intersection. If the momentum of truck A is 9.50 x 104 kg km/h east and the momentum of truck B is 1.05 x 105 kg km/h north, what is the resulting momentum of...

Q:

For your design of a data entry system for Elsinore, take into consideration all the objectives for data entry discussed throughout this chapter. Draw any displays necessary to illustrate your...

Q:

If D 1 = $ 1 . 2 0 , g ( which is constant ) = 7 . 0 % , and P 0 = $ 4 4 , what is the stock's expected dividend yield for the coming year? a . 7 . 0 0 % b . 2 . 5 0 % C . 2 . 9 2 % d . 2 . 7 3 %

Q:

A double-slit arrangement produces interference fringes for sodium light ( = 589 nm) that have an angular separation of 3.50 x 10-3 rad. For what wavelength would the angular separation be 10.0%...

Q:

An 8-kg plunger is released from rest in the position shown and is stopped by two nested springs; the constant of the outer spring is k1 = 3 kN/m and the constant of the inner spring is k2 = 10 kN/m....

Q:

The system shown, consisting of a 20-kg collar A and a 10-kg counterweight B, is at rest when a constant 500-N force is applied to collar A.(a) Determine the velocity of A just before it hits the...

Q:

A 7.5-lb collar is released from rest in the position shown, slides down the inclined rod, and compresses the spring. The direction of motion is reversed and the collar slides up the rod. Knowing...

Q:

Two identical 4-lb collars, A and B, are attached to a spring of constant 7 lb/ft and can slide on a horizontal rod which is free to rotate about a vertical shaft. Collar B is initially prevented...

Q:

An equilibrium mixture of N 2 (g), H 2 (g), and NH 3 (g) is transferred from a 1.50 L flask to a 5.00 L flask. In which direction does a net change occur to restore equilibrium? N(g) + 3 H(g) = 2...

Q:

X[n] is a 1024-point sequence that is nonzero only for 0 ? n ? 1023. Let X[k] be the 1024-point DFT of x[n]. Given X[k], we want to compute x[n] in the ranges 0 ? n ? 3 and 1020 ? 1023 using the...

Q:

In many applications (such as evaluating frequency responses and interpolation), it is of interest to compute the DFT of a short sequence that is ?zero-padded.? In such cases, a specialized ?pruned?...

Q:

In computing the DFT, it is necessary to multiply a complex number by another complex number whose magnitude is unity, i.e., (X + jY) e j? . Clearly, such a complex multiplication changes only the...

Q:

6. Susan figured out a clever way to get 24 samples of monthly returns in just over one year instead of only 12 samples; she takes overlapping samples; that is, the first sample covers Jan. 1 to Feb....

Q:

Calculatiag initial investment Vastine Medical. Inc.. is considering replacing its existing computer system, which was purchased 3 years ago at a cost ot $321,000. The system can be sold today for...

Q:

whats the answer ? Question 5 Weston Mnes has a cost of equity of 140 percent, a pretax cost of debt of 7.3 percent, and a return on assets of 12.6 percent. Ignore taxes What is the debt-equity...