Consider a rigid body of arbitrary shape which is attached at its mass center O and subjected to no force other than its weight and the reaction of the support at O.

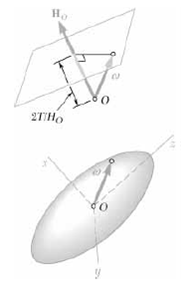
(a) Prove that the angular momentum H_O of the body about the fixed point O is constant in magnitude and direction, that the kinetic energy T of the body is constant, and that the projection along H_O of the angular velocity ω of the body is constant.

(b) Show that the tip of the vector ω describes a curve on a fixed plane in space (called the invariable plane), which is perpendicular to H_O and at a distance 2T/H_O from O.

(c) Show that with respect to a frame of reference attached to the body and coinciding with its principal axes of inertia, the tip of the vector ω appears to describe a curve on an ellipsoid of equation I_xω²_x + I_yω²_y + I_zω²_z = 2T= constant. The ellipsoid (called the Poinsot ellipsoid) is rigidly attached to the body and is of the same shape as the ellipsoid of inertia, but of a different size.

,