Question: Consider a three-dimensional ket space. If a certain set of ortho-normal kets?say, | 1 >, | 2 >, and | 1 > ? are used

Consider a three-dimensional ket space. If a certain set of ortho-normal kets?say, | 1 >, | 2 >, and | 1 > ? are used as the base kets, the operators A and B are represented by with a and b both real.

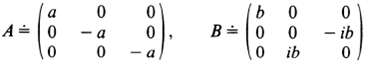
9, B =0 a A =0 - ib a a ib

a. Obviously A exhibits a degenerate spectrum. Does B also exhibit a degenerate spectrum?

b. Show that A and B commute.

c. Find a new set of ortho-normal kets which are simultaneous eigenkets of both A and B. Specify the eigenvalues of A and B for each of the three eigenkets. Does your specification of eigenvalues completely characterize eacheigen ket?

9, B =0 a A =0 - ib a a ib

Step by Step Solution

★★★★★

3.42 Rating (171 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

a The characteristic equation det BAI 0 leads to Xbxb 0 Hence Amb and Ab is a twofoid degenerate ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Document Format (1 attachment)

28-P-M-P-Q-M (165).docx

120 KBs Word File

Students Have Also Explored These Related Modern Physics Questions!

Four pushbuttons (B 0 , B 1 , B 2 , and B 3 ) are used as inputs to a logic circuit. Whenever a button is pushed, it is debounced, after which the circuit loads the button number in binary into a...

Show that if C is represented by r(t) with arbitrary parameter t, then assuming k > 0 asbefore. (23***) T(1) (r' r')(r" r") (r' r")

Consider a simultaneous game in which both players choose between the actions Cooperate, denoted by C, and Defect, denoted by D. A: Suppose that the payoffs in the game are as follows: If both...

Need help to solve this question. Study Notes for the Concept of Rotation Matrix (3) Using different notations for the three principal axes, the position vector can also be 1. Position Vector and its...

Please answer in paragraphs not only bullet points (with explanation for each point). The relevant images for the information are attached below, if any other source is used please cite, but please...

ANSI-SPARC6 Programming Language Compilation Write notes on each of the following topics: (a) the implementation of labels and jumps in a recursive, block structured programming language [7 marks]...

H4 class C is derived from class B (which is derived from base class A). The obj object of class C is defined in the main() function. When the display() function is called, display() in class A is...

What are some of the tangible and intangible capabilities of CrossFit? Based on these capabilities, what are two core competencies? Explain how you decided these are core competencies. In which part...

Poultry Shrimp Asparagus Coconut Oil Almonds Apples Pork Lobster Avocado Olive Oil Cashews Berries Pork Chops Clams Brussel Sprouts Macadamia Oil Hazelnuts Peaches Steak Salmon Carrots Avocado Oil...

This is a java project and I am really frustrated to work on this. I know it is a heavy work and I really need help on this. Please help me. Thank you guys. Packing shapes into fixed size containers...

You want to conduct an experiment with your class to see if students prefer Coke or Pepsi. a. Explain how you could do this, incorporating ideas of blinding and randomization, (i) with a completely...

8. a) Sketch a binary search tree containing ALL of the following English names, and rooted at the name Mae: Zoe, Olivia, Rachel, Emily, Mandy, Dora, Phoebe, Mae, Kit, Denise b. What is the size of...

When confirming accounts receivable, all of the following are true about positive confirmations received from customers, EXCEPT? Select answer from the options below Evidence about the completeness...

Saar Associates sells two licenses to Kim & Company on September 1, 2016. First, in exchange for $100,000, Saar provides Kim with a copy of its proprietary investment management software, which Saar...

Portias Parts Shop recorded the following purchases and sales during the past year: Assume that the company sold all of the June 15 purchase and 100 cases each from the January 1 beginning inventory,...

O'Hara Associates sells golf clubs and with each sale of a full set of clubs provides complementary club-fitting services. A full set of clubs with the fitting services sells for $1,500. O'Hara...

O'Hara Associates sells golf clubs and, with each sale of a full set of clubs, provides complementary club-fitting services. A full set of clubs with the fitting services sells for $1,500. Similar...

O'Hara Associates sells golf clubs, and with each sale of a full set of clubs provides complementary club-fitting services. A full set of clubs with the fitting services sells for $1,500. O'Hara...

To sterilize a 50.0-g glass baby bottle, we must raise its temperature from 22.0C to 95.0C. How much heat transfer is required?

Consider a spinless particle bound to a fixed center by a central force potential. (a) Relate, as much as possible, the matrix elements using only the Wigner-Eckart theorem. Make sure to state under...

Consider a spherical tensor of rank 1 (that is, a vector) Using the expression for d(J=l) given in Problem 3.26, evaluate and show that your results are just what you expect from the transformation...

Express the matrix element in terms of a series in (222\J3|)

Write a program called CozaLozaWoza which prints the numbers 1 to 1 1 0 , 1 1 numbers per line. The program shall print "Coza" in place of the numbers which are multiples of 3 , "Loza" for multiples...

Hoping someone can help me here because my teacher never teach this lesson just handing out a lecture only. Even I search, I am still can't understand. Thank you! 1. The following are the Math final...

The General Hospital is evaluating new office equipment offered by three companies. In each case the interest rate is 15% and the useful life of the equipment is four years. Use NPW analysis to...