Consider a two-variable mathematical programming problem that has the feasible region shown on the graph, where the six dots correspond to CPF solutions. The problem has a linear objective function, and the two dashed lines are objective function lines passing through the optimal solution (4, 5) and the secondbest CPF solution (2, 5). Note that the nonoptimal solution (2, 5) is better than both of its adjacent CPF solutions, which violates Property 3 in Sec. 5.1 for CPF solutions in linear programming. Demonstrate that this problem cannot be a linear programming problem by constructing the feasible region that would result if the six line segments on the boundary were constraint boundaries for linear programming constraints.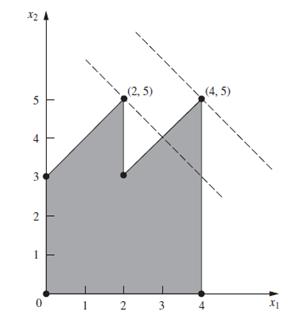

X2 (4, 5) (2, 5) 5 ---- -- 3 4, 2.