Consider an aqueous solution with a high concentration of micelles (Box 25-1) and relatively low concentrations of the fluorescent molecule pyrene and a quencher (cetylpyridinium chloride, designated Q), both of which dissolve in the micelles.

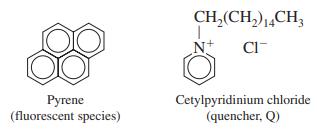
Quenching occurs if pyrene and Q are in the same micelle. Let the total concentration of quencher be [Q] and the concentration of micelles be [M]. The average number of quenchers per micelle is . If Q- is randomly distributed among the micelles, then the probability that a particular micelle has n molecules of Q is given by the Poisson distribution:

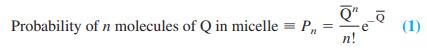
where n! is n factorial (= n[n - 1][n - 2] . . . [1]). The probability that there are no molecules of Q in a micelle is

because 0! ≡ 1.

Let I₀ be the fluorescence intensity of pyrene in the absence of Q and let I_Q be the intensity in the presence of Q (both measured at the same concentration of micelles). The quotient I_Q/I₀ must be e^-Q̅ which is the probability that a micelle does not possess a quencher molecule. Substituting gives Q- = [Q]/[M]gives

Micelles are made of the surfactant molecule, sodium dodecyl sulfate (shown in Problem 18-17). When surfactant is added to a solution, no micelles form until a minimum concentration called the critical micelle concentration (CMC) is attained. When the total concentration of surfactant, [S], exceeds the critical concentration, then the surfactant found in micelles is [S] - [CMC]. The molar concentration of micelles is

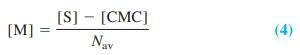
where N_av is the average number of molecules of surfactant in each micelle. Combining Equations 3 and 4 gives an expression for fluorescence as a function of total quencher concentration, [Q]:

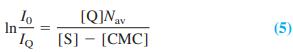
By measuring fluorescence intensity as a function of [Q] at fixed [S], we can find the average number of molecules of S per micelle if we know the critical micelle concentration (which is independently measured in solutions of S). The table gives data for 3.8μ M pyrene in a micellar solution with a total concentration of sodium dodecyl sulfate [S] = 20.8 mM.

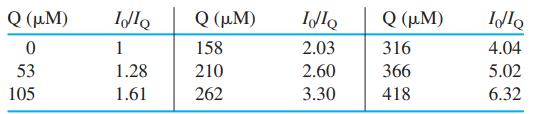
(a) If micelles were not present, quenching would be expected to follow the Stern-Volmer equation 18-25. Show that the graph of I0/IQ versus [Q] is not linear.

(b) The critical micelle concentration is 8.1 mM. Prepare a graph of ln(I₀/I_Q) versus [Q]. Use Equation 5 to find N_av, the average number of sodium dodecyl sulfate molecules per micelle.

(c) Find the concentration of micelles, [M], and the average number of molecules of Q̅ per micelle, when [Q] = 0.200 mM.

(d) Compute the fractions of micelles containing 0, 1, and 2 molecules of Q when [Q] = 0.200 mM.

Equation 18-25

Transcribed Image Text:

CH,(CH,),,CH, N+ CI- Руrene (fluorescent species) Cetylpyridinium chloride (quencher, Q)