Question: Consider a teal, causal sequence x[n] with discrete-time Fourier transform X(e j? ) = X R (e j? ) + jX I (e j? ).

Consider a teal, causal sequence x[n] with discrete-time Fourier transform X(e^j?) = X_R(e^j?) + jX_I(e^j?). The imaginary part of the discrete-time Fourier transform is?

X_I(e^j?) = 3 sin(2?).

Which of the real parts X_Rm(e^j?) listed below are consistent with this information:

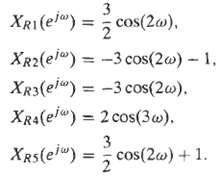
XRI(el) = cos(2@), XR2(el") = -3 cos(2@) - 1, XR3(ei") = -3

XRI(el) = cos(2@), XR2(el") = -3 cos(2@) - 1, XR3(ei") = -3 cos(2w), XR4(el) 2 cos(3w), 3 XRs(ei") = cos(2w) + 1.

Step by Step Solution

★★★★★

3.37 Rating (169 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Document Format (1 attachment)

30-E-T-E-D-S-P (479).docx

120 KBs Word File

Students Have Also Explored These Related Telecommunication Engineering Questions!

The imaginary part of X(e j ) for a casual, real sequence x[n] is X 1 (e j ) = 2 sin 3 sin 4. Additionally, it is known that X(e j )| =0 = 6. Find x[n].

(a) x[n] is a real, causal sequence with the imaginary part of its discrete-time Fourier transform X(e j ) given by Jm{X(e j )} = sin + 2 sin 2. (b) Is your answer to Part (a) unique? If so, explain...

Show that the imaginary part of a complex number z is given by (z - z *)/2i.

Pogram P3.1 can he used to evaluale and plot the DTFT of the farm of E4 33 % Progr P3.1 Evaluation of the % compute the trequescy samples of the TFT aubplot (2,1 0 Chapter 3Discrete-Time Signals in...

Let i and j be positive integers. (i) Prove that there exist natural numbers a and b such that ai = bj+gcd(i, j). You may use standard results provided that you state them clearly. [4 marks] (ii) Let...

Briefly describe ASCII and Unicode and draw attention to any relationship between them. [3 marks] (b) Briefly explain what a Reader is in the context of reading characters from data. [3 marks] A...

Let x[n] be a real causal sequence for which |x[n]|

PLEASE READ ENTIRE QUESTION AND ANSWER USING MATLAB! WILL LEAVE A GOOD REVIEW IF DONE CORRECTLY! Part II: The /magnitude. Ol representation of the frequency domain Begin by obtaining the magnitude, )...

A discrete sequence {xn} can be converted into a continuous representation x(t) = ts X n= (t n ts) xn, where ts is the sampling period. (a) State two characteristic properties of Dirac's function. [2...

Describe how to construct the function cpo ((D E), v) of two cpos (D, vD) and (E, vE). Prove that ((D E), v) is a cpo. (You may use facts about least upper bounds provided you state them clearly.)...

Team as: a1 = carrying play by land a2 = move of air pass and a3 = blitz (I am not sure if this is a offensive asumalo but as well for game purposes).

Suppose consumption rises while investment and government purchases remain constant. How will the AD curve shift in the simple Keynesian model? Under what condition will the rise in Real GDP be equal...

The capital investment committee of Iguana inc. is considering two capitar mestments. The estimated operating income and net cash flows from each investment are as follows: \ begin { tabular } {...

An object whose mass is 300 lb experience changes in its kinetic and potential energies owing to the action of a resultant force R. the work done on the object by the resultant force is 140 Btu....

The 500-lb force acting on the frame is to be resolved into two components acting along the axis of the struts AB and AC. If the components of force along AC are required to be 300 lb, directed from...

A 15-mm-diameter steel bar is to be used as a torsion spring. If the torsional stress in the bar is not to exceed 110 MPa when one end is twisted through an angle of 30, what must be the length of...

A worker on the roof of a house drops her hammer, which slides down the roof at a constant speed of 4 m/s. The roof makes an angle of 30 with the horizontal, and its lowest point is 10 m from the...

Use the conservation of energy to explain why the temperature of a gas increases when it is quickly compressed, whereas the temperature decreases when the gas expands.

What mass of NaCH 3 COO must be dissolved in 0.300 L of 0.25 M CH 3 COOH to produce a solution with pH = 5.09? Assume that the solution volume remains constant at 0.300 L.

Use the differential equation approach to find i(t) for t > 0 in the circuit in Fig. P8 and plot the response including the time interval just prior to opening the switch. t-0 it) 60 +36

Use the differential equation approach to find vc(t) for t > 0 in the circuit in Fig P6.9 and plot the response including the time interval just prior to opening the switch. 12 W + 200 F t-0

Use the differential equation approach to find i(t) for t>0 in the circuit in Fig. P6.4 and plot the response including the time interval just prior to switch movement. it) 10 mA nla

Use the following information on states of the economy and stock returns to calculate the standard deviation of returns. Assuming that all three states are equally likely (Do not round intermediate...

2. Calculator settings Payments Per Year, P/Y The calculator is preset for 1 payment per year (P/Y=1). If you tell the calculator there are 5 $100 payments, it assumes there are $100 annual payments...

Bermuda Triangle Corporation (BTC) currently has 420,000 shares of stock outstanding that sell for $94 per share. Assuming no market imperfections or tax effects exist, what will the share price be...