Question: Consider the following equation: where a is a constant. Show that y(x, t) = A sin(kx - ?t) is not a solution of this equation

Consider the following equation:

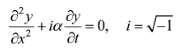
=0, i=-1 dy + ia

where a is a constant. Show that y(x, t) = A sin(kx - ?t) is not a solution of this equation but that the functions y(x, t) = Aei(kx - ?t) and y(x, t) = Aei(kx - ?t) do satisfy that equation.

=0, i=-1 dy + ia

Step by Step Solution

★★★★★

3.26 Rating (161 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

For yx t A sinkx t 2 yx 2 Ak 2 sinkx t and i... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Document Format (1 attachment)

10-P-M-W-M (196).docx

120 KBs Word File

Students Have Also Explored These Related Oscillations Mechanical Waves Questions!

Consider the following equation where the parameter K is nonnegative. (2s + 5)(2s2 + 14s + 49) + Ks (2s +1)(2s + 3) = 0 Determine the poles and zeros, and sketch the root locus plot. Use the plot to...

Consider the following equation where the parameter p is nonnegative. 4s3 + (25 + 5p)s2 + (16 + 30p)s + 40p = 0 Put the equation in standard root locus form and define a suitable root locus parameter...

Consider the following equation of state, expressed in terms of reduced pressure and temperature: What does this equation predict for enthalpy departure from the ideal gas value at the state Pr =...

iii'Question 6 (2 points .What is the value of \"U, -| 'U ? Enter your answer rounded to the nearest hundredth. \fQuestion 8 (5 points) Consider the following equation: tan x + 1 sec x tan x sin x. 2...

MATLAB CODE ANSWERES NEEDED FOR: (a) Solve the problem using fourth-order Runge-Kutta method. (b) Solve the problem using one of the MATLABs built-in functions for solving ODE. Consider vibration of...

Math 2A In-Class Activity Sections 7.8: Laplace Transform 1. We have this spring-mass system with forcing function (): + = (), (0) = (0) = 0 Some possible forcing functions a. b. c. d. () = 1, t 0 ()...

I would like some help to solve this problem and also if you can provide explanations. Introduction to Electromagnetism and Optics 1402 Problem Set 10, due 4/29/24 11:59 pm FEach of these problems...

Littl D2L Myl X P Hor X http x M Pay X Cou X y! call X P Mo X C Jim X C Jim X Unt X y! Jim X + X CO mylab.pearson.com/Student/PlayerTest.aspx?testld=239332837 J M Gmail YouTube Maps PopBlock Plus...

8 Rational Equations Algebra Review Express each sum as a single fraction by finding the least common denominator. 1. 3 I 2. 3. 1 3 I+1 - +5 2 4 z - 9 4. I+3 x2 + 8x + 15 22Practice: Identifying...

PARTIAL DIFFERENTIAL EQUATION QUESTION ANSWER ALL PARTS PLEASE (10 points) For each pair of a flux function, o(z,t), and a source/sink function, f(r.). give the conservation law associated with...

PAWV Power and Light has contracted with a waste disposal firm to have nuclear waste from its nuclear power plants in Pennsylvania disposed of at a government-operated nuclear waste disposal site in...

If you worked at one of Steve Wynn's hotels or resorts, What sort of team building activities would you use for your employees to make sure each of your guests experienced great customer service?

On a class diagram, a ( n ) Access symbol precedes each attribute.Solve the blank

The following are the state diagrams of two DFAs,M 1 andM 2 . Answer the following questions about each of these machines. a. What is the start state? b. What is the set of accept states? c. What...

TearLab Corp. is a health care company that specializes in developing diagnostic devices for eye disease. TearLab reported the following data (in thousands) for three recent years: 1. Determine the...

I guess Ill win that bet! you announced to no one in particular. What bet? Renee asked. Renee Patey was close enough to overhear you. When I bought my REC stock last year Randy insisted it was a...

What are the syntax and semantics of the include construct?

Engineering Structures (July 2013) published a study of the characteristics of fresh concrete. One key variable studied was the time (in hours) needed for pressure stabilization of the concrete. The...

What [I] should be maintained in KI(aq) to produce a solubility of 1.5 x 10 -5 mol PbI 2 /L when PbI 2 (s) is added?

A window washer pushes his scrub brush up a vertical window at constant speed by applying a force F as shown in Fig. 5.65. The brush weighs 12.0 N and the coefficient of kinetic friction is μk =...

The Flying Leap of Flea High-speed motion pictures (3500frames/second) of a jumping 210-μg flea yielded the data to plot the flea's acceleration as a function of time as shown in Fig. 5.66. (See...

A 25,000-kg rocket blasts off vertically from the earth's surface with a constant acceleration. During the motion considered in the problem, assume that g remains constant (see Chapter 12). Inside...

You work for a nuclear research laboratory that is contemplating leasing a diagnostic scanner ( leasing is a common practice with expensive, high - tech equipment ) . The scanner costs $ 4 , 9 0 0 ,...

-You have contacted a number of car dealerships to determine the best interest rate on a new automobile loan. A Ford dealership has quoted you a 5-year, 10% loan in the amount of $35,000 that will...

Harry, Tamara, and Lana were partners under a written agreement made in February that the partnership should continue for ten years. During the same year, Lana, being indebted to Jones, sold and...