Consider the following problem.

Maximize Z = 3x₁ + 7x₂ + 2x₃,

Subject to

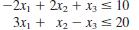
And x₁ ≥ 0, x₂ ≥ 0, x₃ ≥ 0.

You are given the fact that the basic variables in the optimal solution are x₁ and x₃.

(a) Introduce slack variables, and then use the given information to find the optimal solution directly by Gaussian elimination.

(b) Extend the work in part (a) to find the shadow prices.

(c) Use the given information to identify the defining equations of the optimal CPF solution, and then solve these equations to obtain the optimal solution.

(d) Construct the basis matrix B for the optimal BF solution, invert B manually, and then use this B^–1 to solve for the optimal solution and the shadow prices y^*. Then apply the optimality test for the matrix form of the simplex method to verify that this solution is optimal.

(e) Given B^–1 and y^* from part (d), use the fundamental insight presented in Sec. 5.3 to construct the complete final simplex tableau.

+ + x3 2x1 2x2 10