Consider the utility function given by U(x) = ln(x) and the set of gambles with the possible outcomes $10, $20 and $30. For each exercise, it may be useful to use a spreadsheet or other numerical tools.

a. Graph the indifference curves implied by expected utility in the Marschak–Machina triangle. What is the slope of the indifference curves?

b. Now suppose that the decision maker maximizes probability weighted utility, with the weights given by

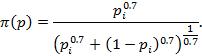
Graph a few examples of indifference curves. What does the probability weighting do to the shape of these curves relative to those in part a?

c. Repeat the exercise in b, now assuming the decision maker maximizes rank-dependent expected utility. Thus, now the probability weighting function is applied to cumulative probabilities.

d. Finally, consider the regret utility function given by

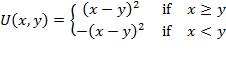
Plot the implied indifference curves supposing the alternative choice would yield $19 with certainty and compare the shape of these curves to those of the other models considered. How do these curves change when the foregone gamble is altered?

- *).