Derivation of the energy equation using integral theorems, in S11.1 the energy equation is derived by accounting for the energy changes occurring in a small rectangular volume element ∆x ∆y ∆z. 

(a) Repeat the derivation using an arbitrary volume element V with a fixed boundary S by following the procedure outlined in Problem 3D.1. Begin by writing the law of conservation of energy as then use the Gauss divergence theorem to convert the surface integral into a volume integral, and obtain Eq. 11.1-6. 

(b) Do the analogous derivation for a moving "blob" of fluid.

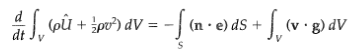
co + po) dV = - (n - e) dS + J_ (v g) dV dt