Ex. 11.3 we assumed the velocity and acceleration were (instantaneously, at least) collinear. Carry out the same analysis for the case where they are perpendicular. Choose your axes so that v lies along the z axis and a along the x axis (Fig. 11.15), so that v = vz, a = ax, and π = sin θ cos Ф x + sin θ sin Ф y + cos θ z. Check that P is consistent with the Lidnard formula. For relativistic velocities (β ?? 1) the radiation is again sharply peaked in the forward direction (Fig. l 1.16). The most important application of these formulas is to circular motion--in this case the radiation is called synchrotron radiation. For a relativistic electron the radiation sweeps around like a locomotive's headlight as the particle moves.]

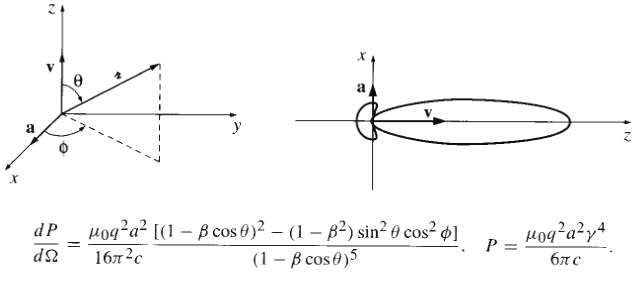
dP ds - y g2a [(1 - B cos 0)2 - (1 - B) sin2 0 cos4] 162c (1 - B cos0)5 P= 2.2.4