Heat flow in a solid bounded by two conical surfaces (Fig. 11B.9). A solid object has the shape depicted in the figure. The conical surfaces θ₁ = constant and θ₂ = constant are held at temperatures T₁ and T₂, respectively. The spherical surface at r = R is insulated. For steady-state heat conduction, find 

(a) The partial differential equation that T(θ) must satisfy. 

(b) The solution to the differential equation in (a) containing two constants of integration. 

(c) Expressions for the constants of integration. 

(d) The expression for the O-component of the heat flux vector. 

(e) The total heat flow (cal/sec) across the conical surface at θ = θ₁.

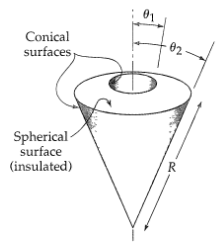
Conical 02 surfaces, Spherical- surface (insulated)