Question: Here??s an exercise in geometry. Theorem 8.5 says that if the moments of inertia of two principal axes are equal, then any axis in the
Here??s an exercise in geometry. Theorem 8.5 says that if the moments of inertia of two principal axes are equal, then any axis in the plane of these axes is a principal axis. This means that the object will rotate happily about any axis in this plane (no torque is needed). Demonstrate this explicitly for four masses m in the shape of a square (which obviously has two moments equal), with the CM as the origin (see Fig). Assume that the masses are connected with strings to the axis, as shown. Your task is to show that the tensions in the strings are such that there is no torque about the center of the square.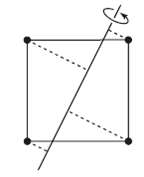
Step by Step Solution
3.40 Rating (162 Votes )
There are 3 Steps involved in it
Label two of the m... View full answer

Get step-by-step solutions from verified subject matter experts
Document Format (1 attachment)
36-P-M-A-M (205).docx
120 KBs Word File


