If the assumptions for a nonpooled t-interval are satisfied, the formula for a (1 )-level upper confidence bound for the difference, 1

If the assumptions for a nonpooled t-interval are satisfied, the formula for a (1− α)-level upper confidence bound for the difference, μ₁ − μ₂, between two population means is

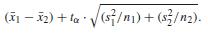
For a left-tailed hypothesis test at the significance level α, the null hypothesis H₀: μ₁ = μ₂ will be rejected in favor of the alternative hypothesis H_a: μ₁ 2 if and only if the (1 − α)-level upper confidence bound for μ₁ − μ₂ is negative. In each case, illustrate the preceding relationship by obtaining the appropriate upper confidence bound and comparing the result to the conclusion of the hypothesis test in the specified exercise.

a. Exercise 10.73

b. Exercise 10.74

(1 ) + le //n) + (s/n2).