If you spin a coin around a vertical diameter on a table, it will slowly lose energy and begin a wobbling motion. The angle between the coin and the table will decrease, and eventually the coin will come to rest. Assume that this process is slow, and consider the motion when the coin makes an angle ? with the table (see Fig). You may assume that the CM is essentially motionless. Let R be the radius of the coin, and let ? be the frequency at which the point of contact on the table traces out its circle. Assume that the coin rolls without slipping.(a) Show that the angular velocity vector of the coin is ? = ? sin ?x2, where x2 points upward along the coin, directly away from the contact point (see Fig.).(b) Show that(c) Show that Abe (or Tom, Franklin, George, John, Dwight, Sue, or Sacagawea) appears to rotate, when viewed from above, with frequency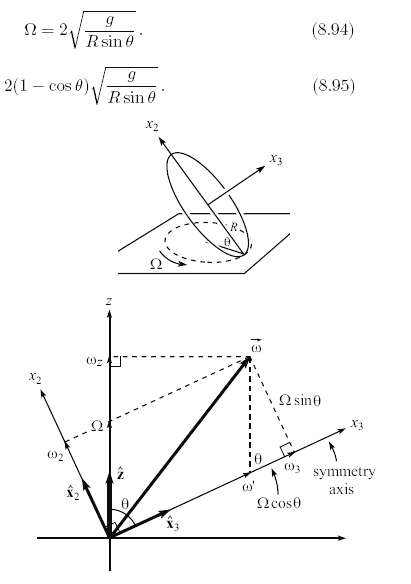

N = 2, (8.94) Rsin 0 (8.95) 2(1 Cos 0) Rsin 0 X2 () X2 Q sine symmetry o' axis Ocos0