Question: In this problem, you are to derive the perpendicular-axis theorem for planar objects, which relates the moments of inertia about two perpendicular axes in the

In this problem, you are to derive the perpendicular-axis theorem for planar objects, which relates the moments of inertia about two perpendicular axes in the plane of Figure to the moment of inertia about a third axis that is perpendicular to the plane of figure. Consider the mass element dm for the figure shown in the xy plane.

(a) Write an expression for the moment of inertia of the figure about the z axis in terms of dm and r.

(b) Relate the distance r of dm to the distances x and y, and show that I_z = I_y + I_x.

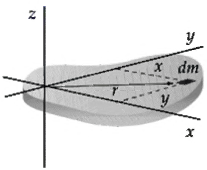
x dm

Step by Step Solution

★★★★★

3.38 Rating (157 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

a b I z r 2 dm x 2 y 2 dm x 2 dm y 2 dm I y I x c Let the z axis be the axis ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Document Format (1 attachment)

10-P-M-R-R (225).docx

120 KBs Word File

Students Have Also Explored These Related Mechanics Questions!

In this problem you will price various options with payoffs based on the Eurostoxx index and the dollar/euro exchange rate. Assume thatQ= 2750 (the index), x = 1.25 ($/=C), s = 0.08 (the exchange...

In this problem you will price various options with payoffs based on the Eurostoxx index and the dollar/euro exchange rate. Assume that Q= 2750 (the index), x = 1.25 ($/=C), s = 0.08 (the exchange...

In this problem you will compute January 12 2004 bid and ask volatilities (using the Black-Scholes implied volatility function) for 1-year IBM options expiring the following January. Note that IBM...

806 Chapter Fifteen OPTIMIZATION: LOCAL AND GLOBAL EXTREMA If f is not continuous or the region R is not closed and bounded, there is no guarantee that f achieves a global maximum or global minimum...

Please help me with the following questions. 1. V FartA A thin, redangular sheet of metal has mass M and sides of length a and b Use the paralleleaxis theorem to Calculate the moment of inertia of...

watch the three short clips below then answer the questions Copy and paste the three links below 1) Projectile Motion https://www.nsf.govews/mmg/mmg_disp.jsp?med_id=72205&from= 2) Newton's Second Law...

g [[3 FigureSkatersand Baseball Bats x Solutrunrorusersrequesi. x l :19 Course: Fall Semester20237CL; x l u Dashboard x | + 6 G \\El...

Questions 1-6 1. A bicycle wheel with a radius of 0.62 m rotates with an angular speed of 24 rad/s about its axle, which is at rest. What is the linear speed of a point on the rim of the wheel? 2....

The simulator will be used to study how cyclists ride at night in low light conditions and in particular how well they can spot hazards. A typical, non-HDR LCD display will be used for the simulator....

Math 1172 Project #4 Applications of Vectors, Coordinate Transformations, and Parameterization by Arclength Due: Thursday, April 13 Name(s): - - - - - - - - - - - - - - - - - - - - Description - - -...

2. A new bridge across the Cumberland River is being planned near a busy high-way intersection in the commercial part of a midwestern town. The construction (first) cost of the bridge is $1,900,000...

A small electric immersion heater is used to heat 61 g of water for a cup of instant coffee. The heater is labeled "90 watts" (it converts electrical energy to thermal energy at this rate). Calculate...

10. LO.4 Describe the conditions under which your client Lee Anne might approach the IRS with an offer in compromise.

Clarence measures the diameter of each tennis ball in a bag with a standard ruler. Unfortunately, he uses the ruler incorrectly so that each of his measurements is 0.2 inch too large. Clarences data...

What kinds of errors can we ignore in student programs?

Use the context of the monopoly-monopsony tension to explain why public employees are so heavily unionized?

Solve these simultaneous equations. a. y = x + 1 y = |x 2 - 2x - 3| b. 2y = x + 4 c. y = 2x y = |2x 2 - 4| = 2 %3D X - 3

Skodel Ltd is a small brewery that is undergoing a major expansion after a takeover by a large European brewery chain. Skodel Ltd produces a range of beers and lagers, and is renowned for the quality...

The missile weighs 40 000 lb. The constant thrust provided by the turbojet engine is T = 15 000 lb. Additional thrust is provided by two rocket boosters B. The propellant in each booster is burned at...

The earthmover initially carries 10m3 of sand having a density of 1520 kg/m3. The sand is unloaded horizontally through a 2.5 m2 dumping port P at a rate of 900 kg/s measured relative to the port....

The 10-Mg helicopter carries a bucket containing 500 kg of water, which is used to fight fires, if is hovers over the land in a fixed position and then releases 50 kg/s of water at 10m/s, measured...

1. (60 pts.) Using the definitions of the hyperbolic functions cosh(x)=21(ex+ex)sinh(x)=21(exex), the basic properties of Laplace transforms, and tables 3.1 and 2.3, find the Laplace transforms,...

The market portfolio ( M ) provides a 1 5 % annual return with a 2 0 % standard deviation. The risk - free rate of return ( r f ) is 5 % per annum. Security Q and P provide 1 7 % and 1 1 % return per...

Assume that the expectations theory fully explains the Treasury Bond Yield Curve. The 10-year zero-coupon bond maturing in 2030 has a yield-to-maturity (YTM) of 3.5%. Assume that instead of simply...