In simple random sampling, we know that a without-replacement sample of size n has smaller variance than a with replacement sample of size n. The same result is not always true for unequal-probability sampling designs (Raj, 1968, p. 56). Consider a with replacement design with selection probabilities ψi, and a corresponding without replacement design with inclusion probabilities πi =nψi; assume nψi

i = 1. . . N.

a. Consider a population with N = 4 and t1 = −5, t2 = 6, t3 = 0, and t4 = −1. The joint inclusion probabilities for a without-replacement sample of size 2 are π12 = 0.004, π13 = π23 = π24 = 0.123, π14 = 0.373, and π34 = 0.254. Find the value of πi for each unit. Show that for this design and population, V (ṫψ)

b. Show that for πi = nψi and V (ṫψ) in (6.8),

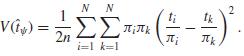
c. Using V (ṫHT) in (6.21), show that if

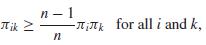
Then V (ṫHT) ≤ V(ṫψ).

d. Gabler (1984) shows that if

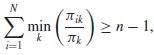
Then V (ṫHT) ≤ V (ṫψ). Show that if πik ≥ (n − 1) πiπk / n for all i and k, then

Gabler’s condition is met.

e. (Requires knowledge of linear algebra.) Show that if V (ṫHT) ≤ V (ṫψ), then

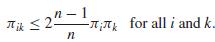
Tk for all i and k. min-1 < 2--TTTk for all i and k.