In their book Empirical Model Building and Response Surfaces (John Wiley, 1987), G. E. P. Box and N. R. Draper describe an experiment with three factors. The data shown in Table 8E.7 are a variation of the original experiment on p. 247 of their book. Suppose that these data were collected in a semiconductor manufacturing process.

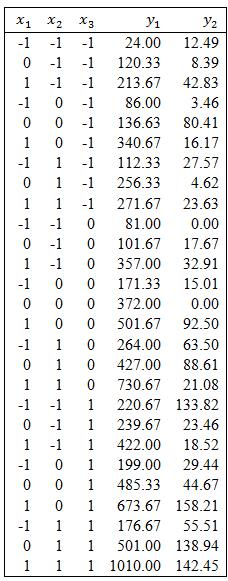
a. The response is the average of three readings on resistivity for a single wafer. Fit a quadratic model to this response.

b. The response is the standard deviation of the three resistivity measurements. Fit a first-order model to this response. 

c. Where would you recommend that we set 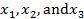 if the objective is to hold mean resistivity at 500 and minimize the standard deviation?

124.00 12.49 0 120.33 8.39 1 213.67 42.83 1 0 86.003.46 0 0 136.63 80.41 1 0340.67 16.17 1 112.33 27.57 0 256.33 4.62 1 271.67 23.63 081.00 0.00 0 1 0 101.67 17.67 1 1 0 357.00 32.91 -1 0 0 171.33 15.01 0 0 0 372.00 0.00 1 0 0 501.67 92.50 264.00 63.50 0 1 0 427.00 88.61 1 1 0 730.67 21.08 220.67 133.82 0 1 239.67 23.46 1 1 422.00 18.52 -1 0 1 199.00 29.44 0 0 485.33 44.67 1 0 673.67 158.21 1 176.67 55.51 0 501.00 138.94 1 1 1 1010.00 142.45 9 3 2