In this problem we derive the formulas used to compute the power spectra of Figure for the five Line codes described in Section 3.7. In the case of each line code, the bit duration is Tb and the pulse amplitude A is conditioned to normalize the average power of the line code o unity as indicated in Figure. Assume that the data stream is randomly generated, and symbols 0 and 1 are equally likely.

Derive the power spectral densities of these line codes as summarized here:

(a) Unipolar non-return-to-zero signals:

(b) Polar non-return-to-zero signals:

(c) Unipolar return-to-zero signals:

(d) Bipolar return-to-zero signals:

(e) Manchester-encoded signals: Hence, confirm the spectral plots displayed inFigure.

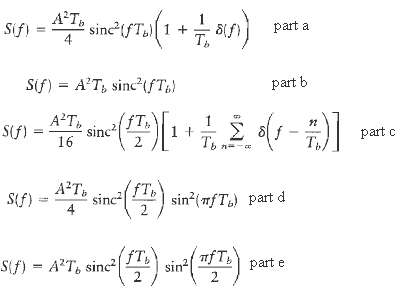
A'T, sinetfT(1 + B) Sif) = part a 4 Sif) = A'T, sinc (ST) part b A'T, sinc 16 fTb |1 + To Sf) part c A'T fT sin (mfT) part d Sf) =4 sinc fTB S(f) = A'T, sinc nf T sin part e