Question: In this problem, you will derive a convenient formula for the speed of sound in air at temperature t in Celsius degrees. Begin by writing

In this problem, you will derive a convenient formula for the speed of sound in air at temperature t in Celsius degrees. Begin by writing the temperature as T = T₀ + ∆T, where T₀ = 273 K corresponds to 0^oC and ∆T = t, the Celsius temperature. The speed of sound is a function of T, v(T). To a first-order approximation, you can write

v(T) ≈ v(T₀) + (dv/dT ) _T0 ∆T,

where (dv/dT)_T₀ is the derivative evaluated at T = T₀. Compute this derivative, and show that the result leads to

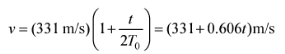
' = (331 m/s)| 1+ 27 (331+0.6061)m/s

Step by Step Solution

★★★★★

3.37 Rating (169 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Since t differs from T only by a... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Document Format (1 attachment)

10-P-M-W-M (191).docx

120 KBs Word File

Students Have Also Explored These Related Oscillations Mechanical Waves Questions!

Derive an expression for the speed of sound based on van der Waals equation of state P = RT(v - b) - a/v2. Using this relation, determine the speed of sound in carbon dioxide at 50C and 200 kPa, and...

In this problem you will compute January 12 2004 bid and ask volatilities (using the Black-Scholes implied volatility function) for 1-year IBM options expiring the following January. Note that IBM...

Derive an expression for the speed of sound based on van der Waals' equation of state P = RT(v - b) - a/v2. Using this relation, determine the speed of sound in carbon dioxide at 808C and 320 kPa,...

Problem 2: Write a simple algorithm that calculates the speed of sound (a) in air of a given temperature (t). For this program you must use this formula: a=1086(5t+297)/247 Note that the formula...

this shiuld be written in c program Problem 2: Write a simple algorithm that calculates the speed of sound (a ) in air of a given temperature (t). For this program you must use this formula:...

Answer all questions and explain 1. 4. The area,A, of a rectangle with length land width w is A = 1w. Find the area ofa rectangle with each length and width. a}l=10m,w=4m b}l=6cm,w=3cm...

2. A sound wave travels in water at speed 1480 mfs for water at temperature 20C. The speed of sound in air is given by the formula van. 2 331 + {1.6 T , where Tis the temperature in Celsius degrees,...

Explain the difference between these two statements: result = 9*2 result = 9*2; The following assignment statements either contain at least one error, or could be improved in some way. Assume that...

2. A sound wave travels in water at speed 1480 m's for water at temperature 20 C. The speed of sound in air is given by the formula Vair = 331 + 0.67 , where 7 is the temperature in Celsius degrees,...

Instuctor's Annotated Edition TENTH EDITION Understandable Statistics Concepts and Methods Charles Henry Brase Regis University Corrinne Pellillo Brase Arapahoe Community College Australia Brazil...

Define each of the following terms: variable cost, fixed cost, step cost, and mixed cost. Give an example of each.

How much would you be willing to pay for a perpetuity that paid a $20 annual payment yesterday, and keeps growing at 5.5% per year, forever? Assume that you can borrow from the bank at a 10% interest...

At the 2008 edition, Carrefour did not support the initiative by means of other marketing communication activities. Build a supporting Carrefour communication plan for the next edition.

One item is omitted in each of the following summaries of balance sheet and income statement data for the following four different corporations: Determine the missing amounts, identifying them by...

Entrepreneurial Publishing Inc. began printing operations on January 1. Jobs 301 and 302 were completed during the month, and all costs applicable to them were recorded on the related cost sheets....

Consider a steel bottle as a CV. It contains carbon dioxide at20C, quality 20%. It has a safety valve that opens at 6 MPa. The bottle is now accidentally heated until the safety valve opens. Write...

Zhou owns a nonrental business with two separate departments. Department A generates net income of $70,000, and Department B generates a net loss of $58,000. Zhou participates 800 hours in the...

No financial decision-maker should ever rely solely on the financial information reported in the annual report to make decisions. It is important to keep abreast of financial news. This activity...

Will precipitation of MgF 2 (s) occur if a 22.5 mg sample of MgCl 2 6 H 2 O is added to 325 mL of 0.035 M KF?

In another version of the "Giant Swing" (see Exercise 5.52), the seat is connected to two cables as shown in Fig. 5.58, one of which is horizontal. The seat swings in a h0ri2ontal circle at a rate of...

A small button placed on a horizontal rotating platform with diameter 0.320 m will revolve with the platform when it is brought up to a speed of 40.0 rev/min, provided the button is no more than...

Rotating Space Stations One problem for humans living in outer space is that they are apparently weightless. One way around this problem is to design a space station that spins about its center at a...

You need a particular piece of equipment for your production process. An equipment-leasing company has offered to lease the equipment to you for $10,000 per year if you sign a guaranteed 5-year lease...

A bridge is expected to have maintenance and repair expenses of $20,000 in the first year. It is expected that these expenses will increase $5,000 per year thereafter during the bridge expected life...

please help me to solve the (d) Katec Corporation borrowed $71,000.00 at 3% compounded quarterly for 14 years to buy a warehouse, Equal payments are made at the end of every 3 months. (a) Determine...