In this problem you will derive an expression for the potential energy of a segment of a string carrying a traveling wave (Figure). The potential energy of a segment equals the work done by the tension in stretching the string, which is ΔU = F(Δℓ - Δx),where F is the tension, Δx is the length of the stretched segment, and Δx is its original length. From the figure we see that

(a) Use the binomial expansion to show that Δℓ - Δx ≈ ½ (Δy/Δx)² Δx, and therefore ΔU ≈ ½ F(Δy/Δx)² Δx

(b) Compute dy/dx from the wave function in Equation. 15-13 and show that  ΔU ≈ ½ Fk² A² cos² (kx - wt)Δx.

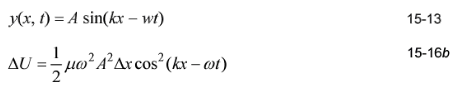
(c) Use F = mv2 and v = w/k to show that your result for (b) is the same as Equation 15-16b.

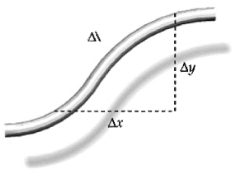
1/2 Al x J(Ax)? + (Ay)? = Ar{1+(Ay/Ax)*}\"2