Let 0 < y 1 < x 1 and set a) Prove that 0 < y n < x n for all n e N.

Let 0 1 1 and set

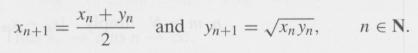
a) Prove that 0 n n for all n e N.

b) Prove that y_n is increasing and bounded above, and that x_n is decreasing and bounded below.

c) Prove that 0 n+1 – y_n+1 1 – y₁)/2ⁿ for n ∊ N.

d) Prove that lim_n→∞ x_n = lim_n→∞ y_n. (This common value is called the arithmetic–geometric mean of x₁ and y₁.)

xn + yn 2and nnEN.