Let the r.v.s X and Y have the Bivariate Normal distribution with parameters μ 1 , μ 2 R,0 < Ï 1 , Ï 2

Let the r.v.s X and Y have the Bivariate Normal distribution with parameters μ₁, μ₂ˆˆ R,0 < σ₁, σ₂< ˆž, and p ˆˆ [-1, 1], and set U = X + Y, V = X - Y.

(i) Verify that É›U = μ₁ + μ₂, Var(U) = σ²₁ + a²₂ + 2pσ₁σ₂,É›V = μ₁ €“ μ₂, Var(V) = σ₁² + σ₂² - 2p σ₁ σ₂, and Cov(U, V) = σ₁² €“ σ₂² (by using Exercises 12 (ii) and 14

(ii) in Chapter 9).

(ii) Since

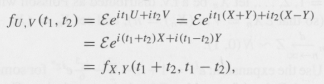
use Exercise 15 in order to conclude that

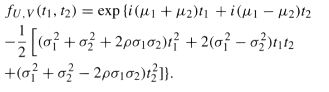
(iii) From part (ii) and Exercise 15, conclude that the r.v.s U and V have the Bivariate Normal distribution with parameters μ₁ + μ₂, μ₁ - μ₂, σ₁² + σ₂² + 2p σ₁ σ₂ = Ï„₁^{2 ,}σ₁² σ₂² - 2p σ₁ σ₂ = Ï„₂², and p(U, V) = (σ₁² €“ σ₂²) /Ï„₁Ï„₂.

(iv) From part (iii) and Exercise 12 (ii) in Chapter 10, conclude that U and V are independent if and only if σ₁ = σ₂.

fu,v (t1, 12) = EeiiU +izV = Eei1(X+Y)+iz(X-Y) = Ee'n+t2)X+i(1-12)Y = fx,y(t1 + 12, t 12), %3D %3D